Posts by Andy Adinets
Data Science
May 21, 2021
Sparse Forests with FIL
Introduction The RAPIDS Forest Inference Library, affectionately known as FIL, dramatically accelerates inference (prediction) for tree-based models, including...
6 MIN READ
Simulation / Modeling / Design
Oct 01, 2014
CUDA Pro Tip: Optimized Filtering with Warp-Aggregated Atomics
Note: This post has been updated (November 2017) for CUDA 9 and the latest GPUs. The NVCC compiler now performs warp aggregation for atomics automatically in...
14 MIN READ
Simulation / Modeling / Design
Jun 12, 2014
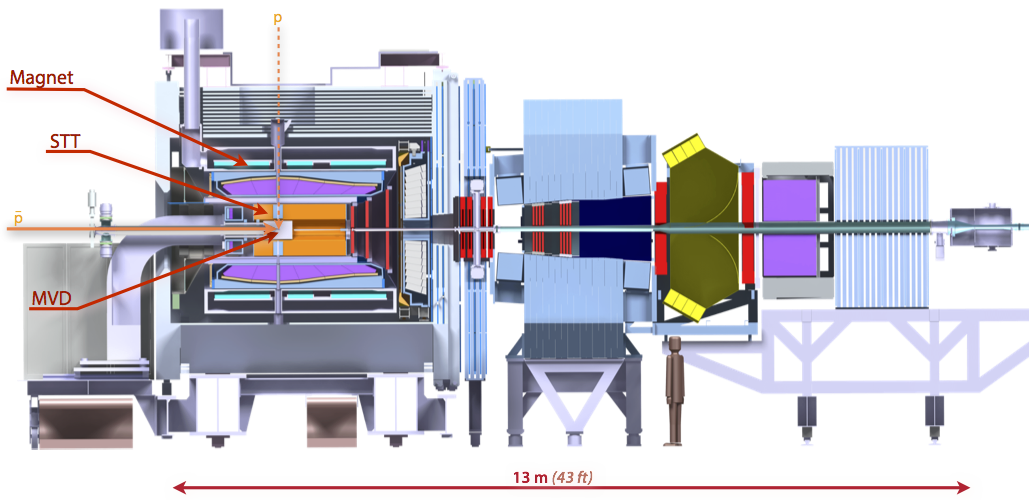
A CUDA Dynamic Parallelism Case Study: PANDA
This post concludes an introductory series on CUDA dynamic parallelism. In this post, I finish the series with a case study on an online track reconstruction...
11 MIN READ
Simulation / Modeling / Design
May 20, 2014
CUDA Dynamic Parallelism API and Principles
This post is the second in a series on CUDA Dynamic Parallelism. In my first post, I introduced Dynamic Parallelism by using it to compute images of the...
13 MIN READ
Simulation / Modeling / Design
May 06, 2014
Adaptive Parallel Computation with CUDA Dynamic Parallelism
Early CUDA programs had to conform to a flat, bulk parallel programming model. Programs had to perform a sequence of kernel launches, and for best performance...
13 MIN READ