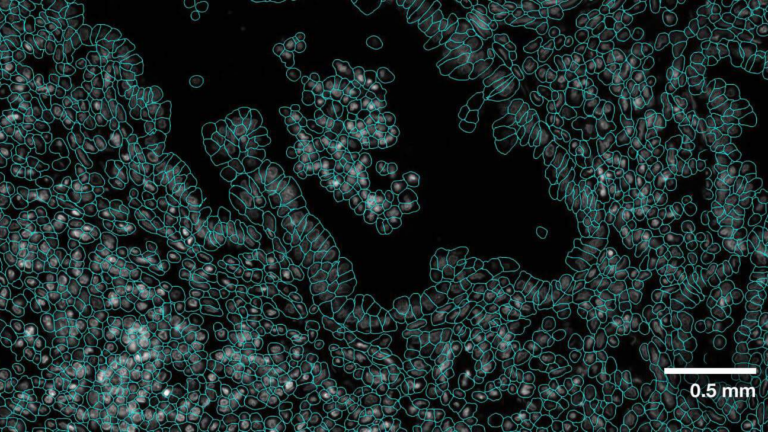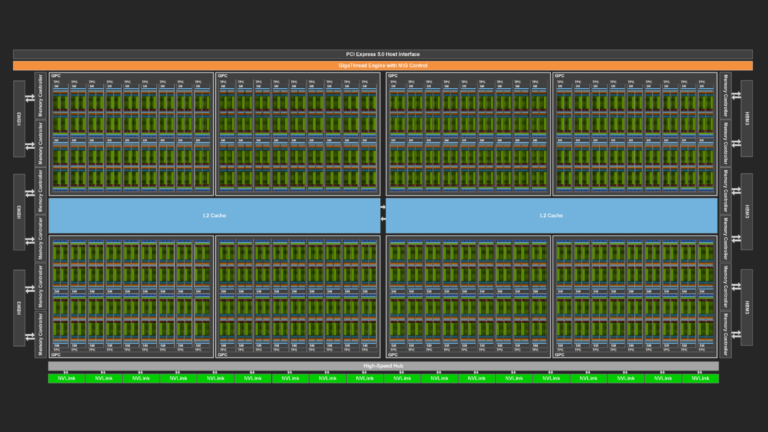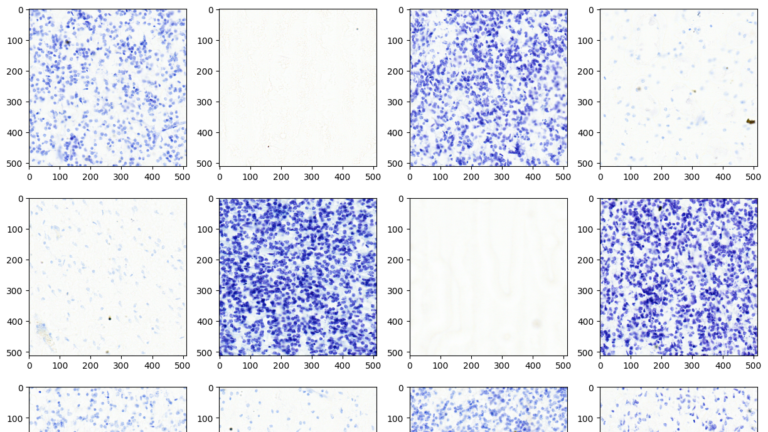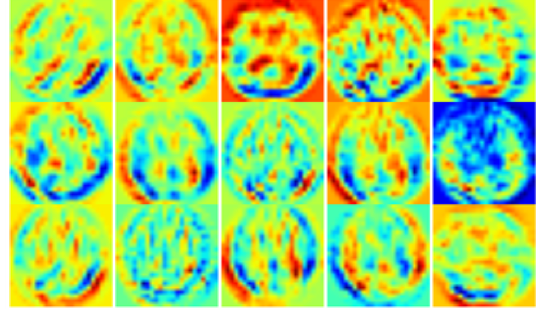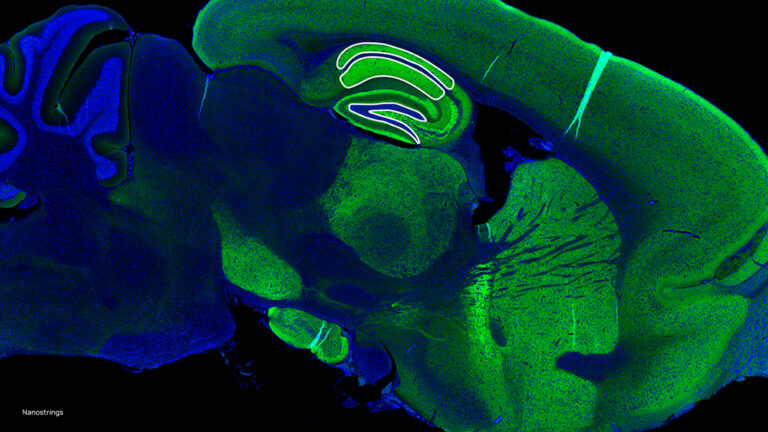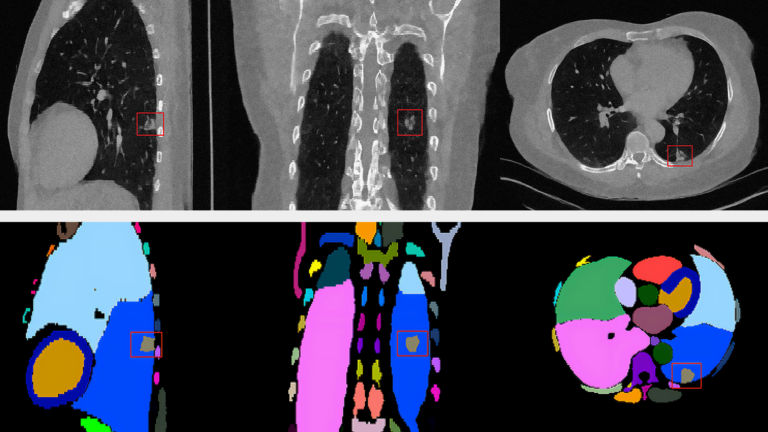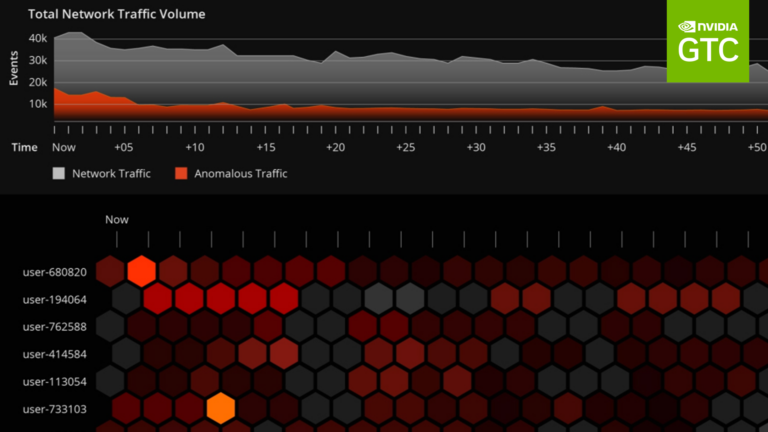
At GTC 2024, experts from NVIDIA and our partners shared insights about GPU-accelerated tools, optimizations, and best practices for data scientists. From the hundreds of sessions covering various topics, we’ve handpicked the top three data science sessions that you won’t want to miss. RAPIDS in 2024: Accelerated Data Science Everywhere Speakers: Dante Gama Dessavre…
]]>