-
Generative AI / LLMsTurbocharging Meta Llama 3 Performance with NVIDIA TensorRT-LLM and NVIDIA Triton Inference Server
-
Conversational AINew Standard for Speech Recognition and Translation from the NVIDIA NeMo Canary Model
-
Top StoriesTurbocharge ASR Accuracy and Speed with NVIDIA NeMo Parakeet-TDT
-
Conversational AIPushing the Boundaries of Speech Recognition with NVIDIA NeMo Parakeet ASR Models
-
Generative AI / LLMsHow Generative AI is Empowering Climate Tech with NVIDIA Earth-2
Recent

Apr 26, 2024
Enhance Text-to-Image Fine-Tuning with DRaFT+, Now Part of NVIDIA NeMo
Text-to-image diffusion models have been established as a powerful method for high-fidelity image generation based on given text. Nevertheless, diffusion models...
10 MIN READ

Apr 25, 2024
Announcing Confidential Computing General Access on NVIDIA H100 Tensor Core GPUs
NVIDIA launched the initial release of the Confidential Computing (CC) solution in private preview for early access in July 2023 through NVIDIA LaunchPad....
3 MIN READ

Apr 23, 2024
Democratizing AI Workflows with Union.ai and NVIDIA DGX Cloud
GPUs were initially specialized for rendering 3D graphics in video games, primarily to accelerate linear algebra calculations. Today, GPUs have become one of...
7 MIN READ

Apr 23, 2024
Webinar: Enhance LLMs with RAG and Accelerate Enterprise AI with Pure Storage and NVIDIA
Join Pure Storage and NVIDIA on April 25 to discover the benefits of enhancing LLMs with RAG for enterprise-scale generative AI applications.
1 MIN READ
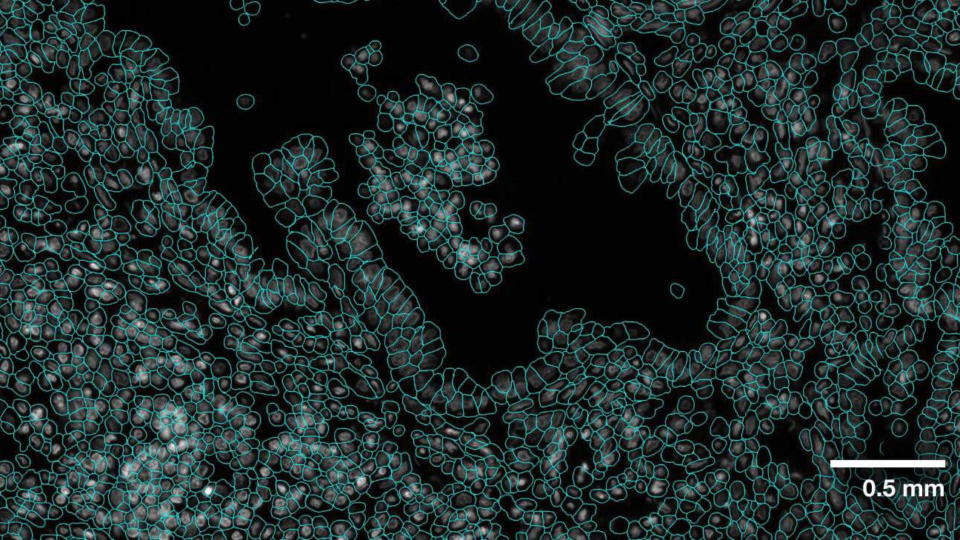
Apr 22, 2024
Advancing Cell Segmentation and Morphology Analysis with NVIDIA AI Foundation Model VISTA-2D
Genomics researchers use different sequencing techniques to better understand biological systems, including single-cell and spatial omics. Unlike single-cell,...
7 MIN READ

Apr 22, 2024
Developing Virtual Factory Solutions with OpenUSD and NVIDIA Omniverse
With NVIDIA AI, NVIDIA Omniverse, and the Universal Scene Description (OpenUSD) ecosystem, industrial developers are building virtual factory solutions that...
4 MIN READ

Apr 22, 2024
Mistral Large and Mixtral 8x22B LLMs Now Powered by NVIDIA NIM and NVIDIA API
This week’s model release features two new NVIDIA AI Foundation models, Mistral Large and Mixtral 8x22B, both developed by Mistral AI. These cutting-edge...
4 MIN READ

Apr 22, 2024
Just Released: NVIDIA Modulus v24.04
Modulus v24.04 delivers an optimized CorrDiff model and Earth2Studio for exploring weather AI models.
1 MIN READ

Apr 22, 2024
Turbocharging Meta Llama 3 Performance with NVIDIA TensorRT-LLM and NVIDIA Triton Inference Server
We're excited to announce support for the Meta Llama 3 family of models in NVIDIA TensorRT-LLM, accelerating and optimizing your LLM inference performance. You...
9 MIN READ

Apr 22, 2024
Enhanced DU Performance and Workload Consolidation for 5G/6G with NVIDIA Aerial CUDA-Accelerated RAN
Aerial CUDA-Accelerated radio access network (RAN) enables acceleration of telco workloads, delivering new levels of spectral efficiency (SE) on a cloud-native...
14 MIN READ
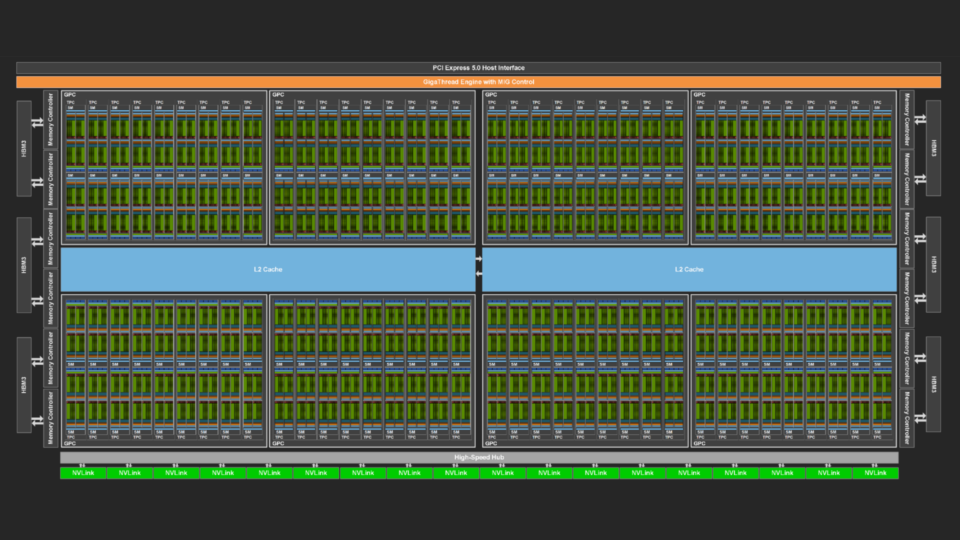
Apr 19, 2024
Measuring the GPU Occupancy of Multi-stream Workloads
NVIDIA GPUs are becoming increasingly powerful with each new generation. This increase generally comes in two forms. Each streaming multi-processor (SM), the...
11 MIN READ

Apr 18, 2024
New Standard for Speech Recognition and Translation from the NVIDIA NeMo Canary Model
NVIDIA NeMo is an end-to-end platform for the development of multimodal generative AI models at scale anywhere—on any cloud and on-premises. The NeMo team...
4 MIN READ
Generative AI / LLMs

Apr 26, 2024
Enhance Text-to-Image Fine-Tuning with DRaFT+, Now Part of NVIDIA NeMo
Text-to-image diffusion models have been established as a powerful method for high-fidelity image generation based on given text. Nevertheless, diffusion models...
10 MIN READ

Apr 25, 2024
Announcing Confidential Computing General Access on NVIDIA H100 Tensor Core GPUs
NVIDIA launched the initial release of the Confidential Computing (CC) solution in private preview for early access in July 2023 through NVIDIA LaunchPad....
3 MIN READ

Apr 23, 2024
Democratizing AI Workflows with Union.ai and NVIDIA DGX Cloud
GPUs were initially specialized for rendering 3D graphics in video games, primarily to accelerate linear algebra calculations. Today, GPUs have become one of...
7 MIN READ

Apr 23, 2024
Webinar: Enhance LLMs with RAG and Accelerate Enterprise AI with Pure Storage and NVIDIA
Join Pure Storage and NVIDIA on April 25 to discover the benefits of enhancing LLMs with RAG for enterprise-scale generative AI applications.
1 MIN READ

Apr 22, 2024
Advancing Cell Segmentation and Morphology Analysis with NVIDIA AI Foundation Model VISTA-2D
Genomics researchers use different sequencing techniques to better understand biological systems, including single-cell and spatial omics. Unlike single-cell,...
7 MIN READ

Apr 22, 2024
Mistral Large and Mixtral 8x22B LLMs Now Powered by NVIDIA NIM and NVIDIA API
This week’s model release features two new NVIDIA AI Foundation models, Mistral Large and Mixtral 8x22B, both developed by Mistral AI. These cutting-edge...
4 MIN READ

Apr 22, 2024
Turbocharging Meta Llama 3 Performance with NVIDIA TensorRT-LLM and NVIDIA Triton Inference Server
We're excited to announce support for the Meta Llama 3 family of models in NVIDIA TensorRT-LLM, accelerating and optimizing your LLM inference performance. You...
9 MIN READ

Apr 18, 2024
Turbocharge ASR Accuracy and Speed with NVIDIA NeMo Parakeet-TDT
NVIDIA NeMo, an end-to-end platform for developing multimodal generative AI models at scale anywhere—on any cloud and on-premises—recently released...
6 MIN READ

Apr 18, 2024
Pushing the Boundaries of Speech Recognition with NVIDIA NeMo Parakeet ASR Models
NVIDIA NeMo, an end-to-end platform for the development of multimodal generative AI models at scale anywhere—on any cloud and on-premises—released the...
6 MIN READ
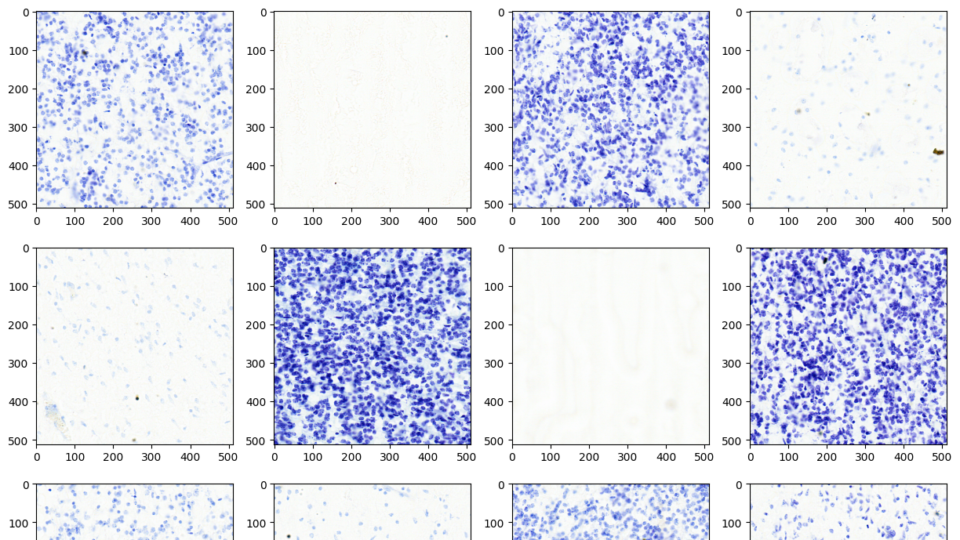
Apr 17, 2024
Advancing Medical Image Decoding with GPU-Accelerated nvImageCodec
This post delves into the capabilities of decoding DICOM medical images within AWS HealthImaging using the nvJPEG2000 library. We'll guide you through the...
16 MIN READ

Apr 10, 2024
How Generative AI is Empowering Climate Tech with NVIDIA Earth-2
In the context of global warming, NVIDIA Earth-2 has emerged as a pivotal platform for climate tech, generating actionable insights in the face of increasingly...
14 MIN READ

Apr 05, 2024
Explainer: What Is Retrieval-Augmented Generation?
Retrieval-augmented generation enhances large language model prompts with relevant data for more practical, accurate responses.
1 MIN READ
Simulation / Modeling / Design

Apr 22, 2024
Just Released: NVIDIA Modulus v24.04
Modulus v24.04 delivers an optimized CorrDiff model and Earth2Studio for exploring weather AI models.
1 MIN READ

Apr 22, 2024
Developing Virtual Factory Solutions with OpenUSD and NVIDIA Omniverse
With NVIDIA AI, NVIDIA Omniverse, and the Universal Scene Description (OpenUSD) ecosystem, industrial developers are building virtual factory solutions that...
4 MIN READ

Apr 22, 2024
Enhanced DU Performance and Workload Consolidation for 5G/6G with NVIDIA Aerial CUDA-Accelerated RAN
Aerial CUDA-Accelerated radio access network (RAN) enables acceleration of telco workloads, delivering new levels of spectral efficiency (SE) on a cloud-native...
14 MIN READ

Apr 11, 2024
New Video Series: OpenUSD for Developers
Universal Scene Description, also called OpenUSD or USD, is an open and extensible framework for creating, editing, querying, rendering, collaborating, and...
3 MIN READ

Apr 10, 2024
How Generative AI is Empowering Climate Tech with NVIDIA Earth-2
In the context of global warming, NVIDIA Earth-2 has emerged as a pivotal platform for climate tech, generating actionable insights in the face of increasingly...
14 MIN READ

Mar 27, 2024
Efficient CUDA Debugging: Using NVIDIA Compute Sanitizer with NVIDIA Tools Extension and Creating Custom Tools
NVIDIA Compute Sanitizer is a powerful tool that can save you time and effort while improving the reliability and performance of your CUDA applications....
14 MIN READ

Mar 25, 2024
Building High-Performance Applications in the Era of Accelerated Computing
AI is augmenting high-performance computing (HPC) with novel approaches to data processing, simulation, and modeling. Because of the computational requirements...
6 MIN READ
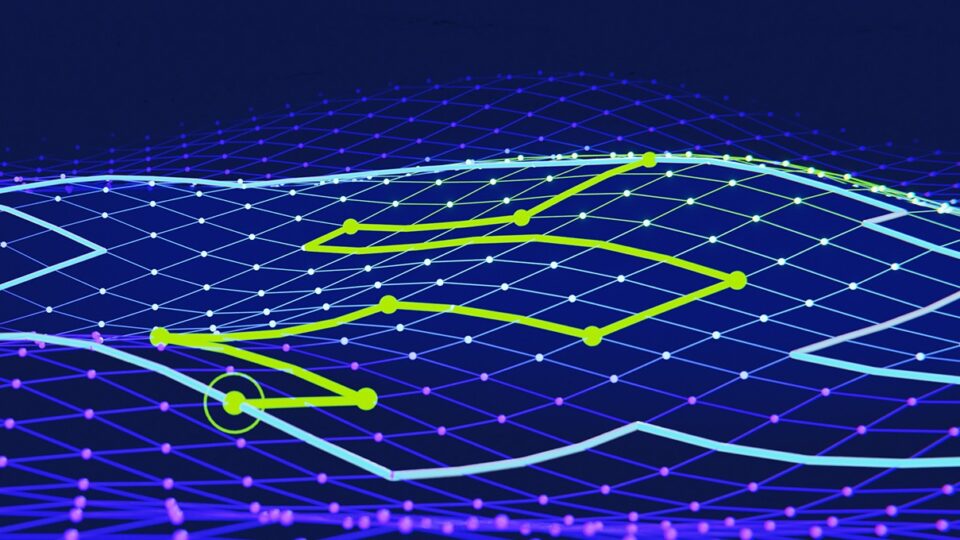
Mar 20, 2024
Record-Breaking NVIDIA cuOpt Algorithms Deliver Route Optimization Solutions 100x Faster
NVIDIA cuOpt is an accelerated optimization engine for solving complex routing problems. It efficiently solves problems with different aspects such as breaks,...
13 MIN READ

Mar 20, 2024
Accelerating the Future of Wireless Communication with the NVIDIA 6G Developer Program
6G will make the telco network AI-native for the first time. To develop 6G technologies, the telecom industry needs a whole new approach to research. The...
10 MIN READ

Mar 19, 2024
Generative AI for Digital Humans and New AI-powered NVIDIA RTX Lighting
At GDC 2024, NVIDIA announced that leading AI application developers such as Inworld AI are using NVIDIA digital human technologies to accelerate the deployment...
5 MIN READ

Mar 18, 2024
NVIDIA GB200 NVL72 Delivers Trillion-Parameter LLM Training and Real-Time Inference
What is the interest in trillion-parameter models? We know many of the use cases today and interest is growing due to the promise of an increased capacity for:...
9 MIN READ

Mar 13, 2024
An Introduction to Quantum Accelerated Supercomputing
The development of useful quantum computing is a massive global effort, spanning government, enterprise, and academia. The benefits of quantum computing could...
10 MIN READ
Conversational AI

Apr 18, 2024
New Standard for Speech Recognition and Translation from the NVIDIA NeMo Canary Model
NVIDIA NeMo is an end-to-end platform for the development of multimodal generative AI models at scale anywhere—on any cloud and on-premises. The NeMo team...
4 MIN READ

Apr 18, 2024
Turbocharge ASR Accuracy and Speed with NVIDIA NeMo Parakeet-TDT
NVIDIA NeMo, an end-to-end platform for developing multimodal generative AI models at scale anywhere—on any cloud and on-premises—recently released...
6 MIN READ

Apr 18, 2024
Pushing the Boundaries of Speech Recognition with NVIDIA NeMo Parakeet ASR Models
NVIDIA NeMo, an end-to-end platform for the development of multimodal generative AI models at scale anywhere—on any cloud and on-premises—released the...
6 MIN READ
Apr 12, 2024
Explainer: What Is a Convolutional Neural Network?
A convolutional neural network is a type of deep learning network used primarily to identify and classify images and to recognize objects within images.
1 MIN READ
Mar 27, 2024
Develop Custom Enterprise Generative AI with NVIDIA NeMo
Generative AI is transforming computing, paving new avenues for humans to interact with computers in natural, intuitive ways. For enterprises, the prospect of...
14 MIN READ

Mar 19, 2024
Generative AI for Digital Humans and New AI-powered NVIDIA RTX Lighting
At GDC 2024, NVIDIA announced that leading AI application developers such as Inworld AI are using NVIDIA digital human technologies to accelerate the deployment...
5 MIN READ

Mar 19, 2024
NVIDIA Speech and Translation AI Models Set Records for Speed and Accuracy
Speech and translation AI models developed at NVIDIA are pushing the boundaries of performance and innovation. The NVIDIA Parakeet automatic speech recognition...
8 MIN READ
Mar 06, 2024
Turning Machine Learning to Federated Learning in Minutes with NVIDIA FLARE 2.4
Federated learning (FL) is experiencing accelerated adoption due to its decentralized, privacy-preserving nature. In sectors such as healthcare and financial...
16 MIN READ

Mar 04, 2024
Solve Complex AI Tasks with Leaderboard-Topping Smaug 72B from NVIDIA AI Foundation Models
This week’s model release features the NVIDIA-optimized language model Smaug 72B, which you can experience directly from your browser. NVIDIA AI Foundation...
2 MIN READ

Feb 29, 2024
Scalable Federated Learning with NVIDIA FLARE for Enhanced LLM Performance
In the ever-evolving landscape of large language models (LLMs), effective data management is a key challenge. Data is at the heart of model performance. While...
8 MIN READ

Feb 29, 2024
Event: Speech and Generative AI Developer Day at NVIDIA GTC 2024
Learn how to build a RAG-powered application with a human voice interface at NVIDIA GTC 2024 Speech and Generative AI Developer Day.
1 MIN READ

Feb 28, 2024
Unlock Your LLM Coding Potential with StarCoder2
Coding is essential in the digital age, but it can also be tedious and time-consuming. That's why many developers are looking for ways to automate and...
7 MIN READ
Computer Vision / Video Analytics

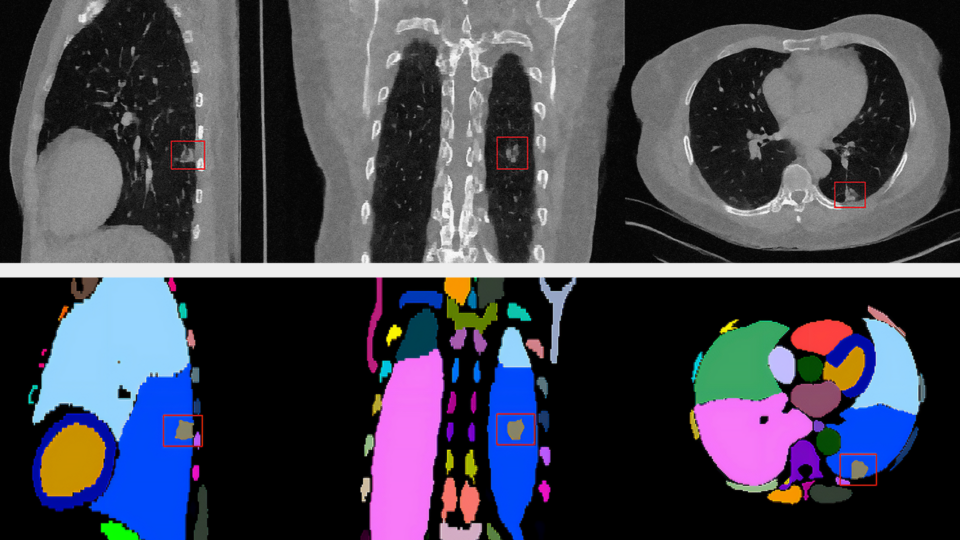
Apr 17, 2024
Advancing Medical Image Decoding with GPU-Accelerated nvImageCodec
This post delves into the capabilities of decoding DICOM medical images within AWS HealthImaging using the nvJPEG2000 library. We'll guide you through the...
16 MIN READ

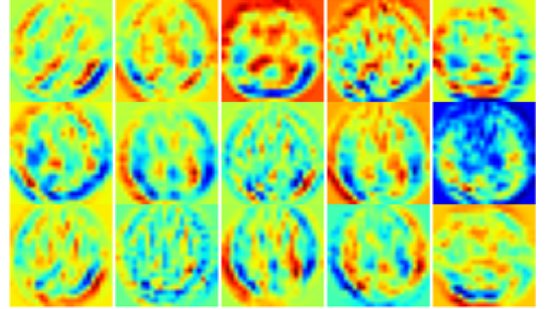
Apr 12, 2024
Explainer: What Is a Convolutional Neural Network?
A convolutional neural network is a type of deep learning network used primarily to identify and classify images and to recognize objects within images.
1 MIN READ

Mar 22, 2024
Explainer: What Is Computer Vision?
Computer vision defines the field that enables devices to acquire, process, understand, and analyze digital images and videos and extract useful...
1 MIN READ
Mar 20, 2024
Developing Production-Ready AI Sensor Processing Applications with NVIDIA Holoscan 1.0
Edge AI developers are building AI applications and products for safety-critical and regulated use cases. With NVIDIA Holoscan 1.0, these applications can...
7 MIN READ
Mar 19, 2024
Breaking Barriers in Healthcare with New Models for Generative AI and Cellular Imaging
Driving the future of healthcare imaging, NVIDIA MONAI microservices are creating unique state-of-the-art models and expanded modalities to meet the demands of...
4 MIN READ

Mar 12, 2024
Calculating Video Quality Using NVIDIA GPUs and VMAF-CUDA
Video quality metrics are used to evaluate the fidelity of video content. They provide a consistent quantitative measurement to assess the performance of the...
14 MIN READ

Mar 08, 2024
cuTENSOR 2.0: Applications and Performance
While part 1 focused on the usage of the new NVIDIA cuTENSOR 2.0 CUDA math library, this post introduces a variety of usage modes beyond that, specifically...
9 MIN READ

Mar 08, 2024
cuTENSOR 2.0: A Comprehensive Guide for Accelerating Tensor Computations
NVIDIA cuTENSOR is a CUDA math library that provides optimized implementations of tensor operations where tensors are dense, multi-dimensional arrays or array...
17 MIN READ

Mar 07, 2024
Generate Stunning Images with Stable Diffusion XL on the NVIDIA AI Inference Platform
Diffusion models are transforming creative workflows across industries. These models generate stunning images based on simple text or image inputs by...
14 MIN READ

Mar 06, 2024
Featured Smart Spaces Sessions at NVIDIA GTC 2024
From cities and airports to Olympic Stadiums, AI is transforming public spaces into safer, smarter, and more sustainable environments.
1 MIN READ

Mar 05, 2024
Spotlight: Honeywell Accelerates Industrial Process Simulation with NVIDIA cuDSS
For over a decade, traditional industrial process modeling and simulation approaches have struggled to fully leverage multicore CPUs or acceleration devices to...
8 MIN READ

Feb 29, 2024
Top Synthetic Data Generation Sessions at NVIDIA GTC 2024
Learn how synthetic data is supercharging 3D simulation and computer vision workflows, from visual inspection to autonomous machines.
1 MIN READ
Data Science

Apr 23, 2024
Democratizing AI Workflows with Union.ai and NVIDIA DGX Cloud
GPUs were initially specialized for rendering 3D graphics in video games, primarily to accelerate linear algebra calculations. Today, GPUs have become one of...
7 MIN READ

Apr 22, 2024
Advancing Cell Segmentation and Morphology Analysis with NVIDIA AI Foundation Model VISTA-2D
Genomics researchers use different sequencing techniques to better understand biological systems, including single-cell and spatial omics. Unlike single-cell,...
7 MIN READ

Apr 17, 2024
Advancing Medical Image Decoding with GPU-Accelerated nvImageCodec
This post delves into the capabilities of decoding DICOM medical images within AWS HealthImaging using the nvJPEG2000 library. We'll guide you through the...
16 MIN READ

Apr 12, 2024
Explainer: What Is a Convolutional Neural Network?
A convolutional neural network is a type of deep learning network used primarily to identify and classify images and to recognize objects within images.
1 MIN READ

Apr 11, 2024
New Video Series: OpenUSD for Developers
Universal Scene Description, also called OpenUSD or USD, is an open and extensible framework for creating, editing, querying, rendering, collaborating, and...
3 MIN READ

Apr 05, 2024
Explainer: What Is Retrieval-Augmented Generation?
Retrieval-augmented generation enhances large language model prompts with relevant data for more practical, accurate responses.
1 MIN READ
Apr 03, 2024
Optimizing Memory and Retrieval for Graph Neural Networks with WholeGraph, Part 2
Large-scale graph neural network (GNN) training presents formidable challenges, particularly concerning the scale and complexity of graph data. These challenges...
5 MIN READ
Mar 29, 2024
Explainer: What Is Sentiment Analysis?
Sentiment analysis is the automated interpretation and classification of emotions (usually positive, negative, or neutral) from textual data such as written...
1 MIN READ

Mar 27, 2024
Efficient CUDA Debugging: Using NVIDIA Compute Sanitizer with NVIDIA Tools Extension and Creating Custom Tools
NVIDIA Compute Sanitizer is a powerful tool that can save you time and effort while improving the reliability and performance of your CUDA applications....
14 MIN READ

Mar 27, 2024
New Self-Paced Course: Accelerate Data Science Workflows with Zero Code Changes
Learn how to use RAPIDS to speed up your CPU-based data science workflows.
1 MIN READ

Mar 27, 2024
Scale and Curate High-Quality Datasets for LLM Training with NVIDIA NeMo Curator
Enterprises are using large language models (LLMs) as powerful tools to improve operational efficiency and drive innovation. NVIDIA NeMo microservices aim to...
6 MIN READ
Mar 21, 2024
Speed Up Your AI Development: NVIDIA AI Workbench Goes GA
NVIDIA AI Workbench, a toolkit for AI and ML developers, is now generally available as a free download. It features automation that removes roadblocks for...
4 MIN READ
Content Creation / Rendering

Apr 11, 2024
New Video Series: OpenUSD for Developers
Universal Scene Description, also called OpenUSD or USD, is an open and extensible framework for creating, editing, querying, rendering, collaborating, and...
3 MIN READ

Apr 09, 2024
Next-Generation Live Media Apps on Repurposable Clusters with NVIDIA Holoscan for Media
NVIDIA Holoscan for Media is now available to all developers looking to build next-generation live media applications on fully repurposable clusters. ...
4 MIN READ

Mar 21, 2024
Speed Up Your AI Development: NVIDIA AI Workbench Goes GA
NVIDIA AI Workbench, a toolkit for AI and ML developers, is now generally available as a free download. It features automation that removes roadblocks for...
4 MIN READ

Mar 21, 2024
Upgrade Your Graphics: Explore New Ray Tracing Features for NVIDIA Nsight Tools
The union of ray tracing and AI is pushing graphics fidelity and performance to new heights. Helping you build optimized, bug-free applications in this era of...
5 MIN READ

Mar 19, 2024
Generative AI for Digital Humans and New AI-powered NVIDIA RTX Lighting
At GDC 2024, NVIDIA announced that leading AI application developers such as Inworld AI are using NVIDIA digital human technologies to accelerate the deployment...
5 MIN READ

Mar 14, 2024
Powerful Shader Insights: Using Shader Debug Info with NVIDIA Nsight Graphics
As ray tracing becomes the predominant rendering technique in modern game engines, a single GPU RayGen shader can now perform most of the light simulation of a...
7 MIN READ

Mar 12, 2024
Streamline Live Media Application Development with New Features in NVIDIA Holoscan for Media
NVIDIA Holoscan for Media is a software-defined platform for building and deploying applications for live media. Recent updates introduce a user-friendly...
5 MIN READ

Mar 11, 2024
Advancing GPU-Driven Rendering with Work Graphs in Direct3D 12
GPU-driven rendering has long been a major goal for many game applications. It enables better scalability for handling large virtual scenes and reduces cases...
12 MIN READ
Mar 11, 2024
Work Graphs in Direct3D 12: A Case Study of Deferred Shading
When it comes to game application performance, GPU-driven rendering enables better scalability for handling large virtual scenes. Direct3D 12 (D3D12) introduces...
14 MIN READ

Mar 07, 2024
Top Video Streaming and Conferencing Sessions at NVIDIA GTC 2024
Learn how AI and NVIDIA Maxine are transforming the video streaming and conferencing industry.
1 MIN READ

Mar 07, 2024
Make the Most of NVIDIA GTC 2024 with In-Person, Hands-On Learning
We are so excited to be back in person at GTC this year at the San Jose Convention Center. With thousands of developers, industry leaders, researchers, and...
6 MIN READ

Feb 29, 2024
Video Series: Getting Started with Universal Scene Description (OpenUSD)
Gain a foundational understanding of USD, the open and extensible framework for creating, editing, querying, rendering, collaborating, and simulating within 3D...
1 MIN READ
Robotics

Apr 22, 2024
Developing Virtual Factory Solutions with OpenUSD and NVIDIA Omniverse
With NVIDIA AI, NVIDIA Omniverse, and the Universal Scene Description (OpenUSD) ecosystem, industrial developers are building virtual factory solutions that...
4 MIN READ

Mar 20, 2024
Developing Production-Ready AI Sensor Processing Applications with NVIDIA Holoscan 1.0
Edge AI developers are building AI applications and products for safety-critical and regulated use cases. With NVIDIA Holoscan 1.0, these applications can...
7 MIN READ

Mar 20, 2024
Record-Breaking NVIDIA cuOpt Algorithms Deliver Route Optimization Solutions 100x Faster
NVIDIA cuOpt is an accelerated optimization engine for solving complex routing problems. It efficiently solves problems with different aspects such as breaks,...
13 MIN READ

Mar 18, 2024
Scale AI-Enabled Robotics Development Workloads with NVIDIA OSMO
Autonomous machine development is an iterative process of data generation and gathering, model training, and deployment characterized by complex multi-stage,...
4 MIN READ

Mar 07, 2024
Make the Most of NVIDIA GTC 2024 with In-Person, Hands-On Learning
We are so excited to be back in person at GTC this year at the San Jose Convention Center. With thousands of developers, industry leaders, researchers, and...
6 MIN READ

Feb 29, 2024
Top Synthetic Data Generation Sessions at NVIDIA GTC 2024
Learn how synthetic data is supercharging 3D simulation and computer vision workflows, from visual inspection to autonomous machines.
1 MIN READ

Feb 26, 2024
Detecting Real-Time Waste Contamination Using Edge Computing and Video Analytics
The past few decades have witnessed a surge in rates of waste generation, closely linked to economic development and urbanization. This escalation in waste...
8 MIN READ

Feb 26, 2024
Developer Days at NVIDIA GTC 2024
Connect with industry leaders, learn from technical experts, and collaborate with peers at NVIDIA GTC 2024 Developer Days.
1 MIN READ
Feb 21, 2024
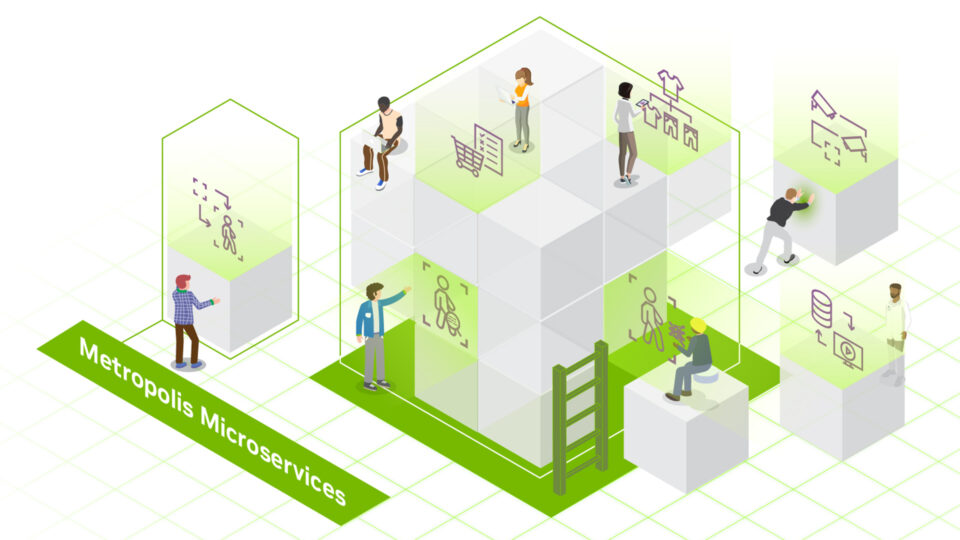
Webinar: Accelerate Edge AI Development With NVIDIA Metropolis Microservices For Jetson
On March 5, 8am PT, learn how NVIDIA Metropolis microservices for Jetson Orin helps you modernize your app stack, streamline development and deployment, and...
1 MIN READ
Feb 19, 2024
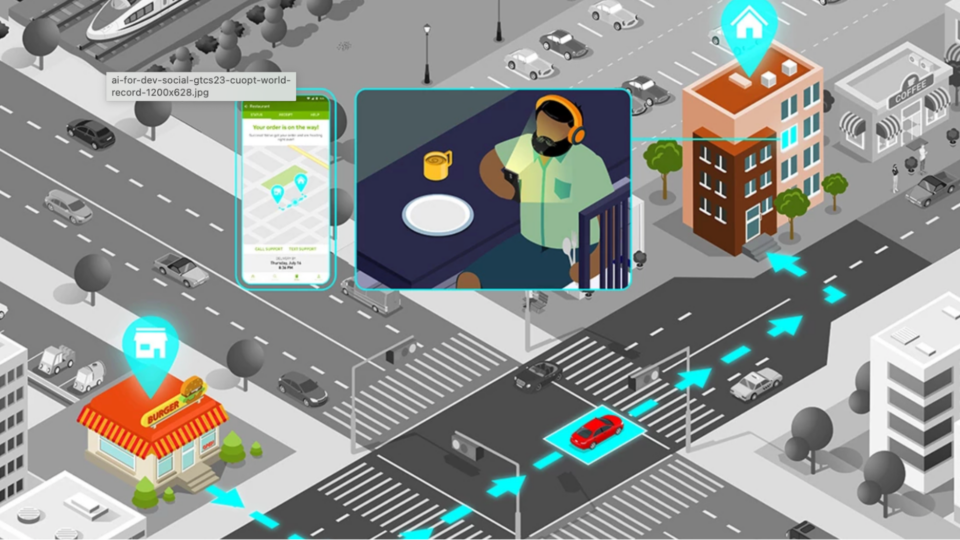
Experience NVIDIA cuOpt Accelerated Optimization to Boost Operational Efficiency
This week’s model release features NVIDIA cuOpt, a world-record-breaking accelerated optimization engine that helps teams solve complex routing problems and...
6 MIN READ

Feb 13, 2024
Upcoming Event: OpenUSD Day at NVIDIA GTC 2024
On March 19, learn how to build generative AI-enabled 3D pipelines and tools using Universal Scene Description for industrial digitalization.
1 MIN READ
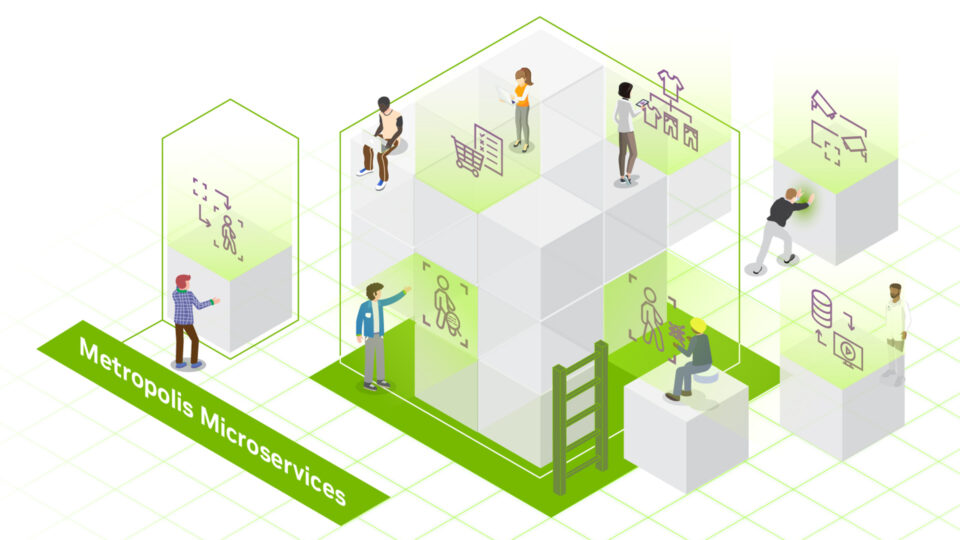
Jan 25, 2024
Announcing NVIDIA Metropolis Microservices for Jetson for Rapid Edge AI Development
Building vision AI applications for the edge often comes with notoriously long and costly development cycles. At the same time, quickly developing edge AI...
6 MIN READ
Edge Computing

Apr 22, 2024
Enhanced DU Performance and Workload Consolidation for 5G/6G with NVIDIA Aerial CUDA-Accelerated RAN
Aerial CUDA-Accelerated radio access network (RAN) enables acceleration of telco workloads, delivering new levels of spectral efficiency (SE) on a cloud-native...
14 MIN READ

Mar 20, 2024
Powering Mission-Critical AI at the Edge with NVIDIA AI Enterprise IGX
NVIDIA SDKs have been instrumental in accelerating AI applications across a spectrum of use cases spanning smart cities, medical, and robotics. However,...
6 MIN READ

Mar 20, 2024
Developing Production-Ready AI Sensor Processing Applications with NVIDIA Holoscan 1.0
Edge AI developers are building AI applications and products for safety-critical and regulated use cases. With NVIDIA Holoscan 1.0, these applications can...
7 MIN READ

Mar 20, 2024
Accelerating the Future of Wireless Communication with the NVIDIA 6G Developer Program
6G will make the telco network AI-native for the first time. To develop 6G technologies, the telecom industry needs a whole new approach to research. The...
10 MIN READ

Mar 05, 2024
Spotlight: Honeywell Accelerates Industrial Process Simulation with NVIDIA cuDSS
For over a decade, traditional industrial process modeling and simulation approaches have struggled to fully leverage multicore CPUs or acceleration devices to...
8 MIN READ

Mar 01, 2024
Featured Energy Sessions at NVIDIA GTC 2024
Hear from ExxonMobil, Honeywell, Siemens Energy, and more as they explore AI and HPC innovation in oil, gas, power, and utilities.
1 MIN READ

Mar 01, 2024
Top Telecom Sessions at NVIDIA GTC 2024
Hear from Amdocs, Indosat, KT, NTT, ServiceNow, Singtel, SoftBank, and Verizon, plus a special address from NVIDIA at GTC. Explore AI transforming customer...
1 MIN READ

Feb 26, 2024
Detecting Real-Time Waste Contamination Using Edge Computing and Video Analytics
The past few decades have witnessed a surge in rates of waste generation, closely linked to economic development and urbanization. This escalation in waste...
8 MIN READ

Feb 21, 2024
Top Computer Vision/Video Analytics Sessions at NVIDIA GTC 2024
Discover the transformative power of computer vision and video analytics at GTC. Dive into cutting-edge techniques such as vision transformers, AI agents,...
1 MIN READ

Feb 21, 2024
Webinar: Accelerate Edge AI Development With NVIDIA Metropolis Microservices For Jetson
On March 5, 8am PT, learn how NVIDIA Metropolis microservices for Jetson Orin helps you modernize your app stack, streamline development and deployment, and...
1 MIN READ

Jan 29, 2024
Emulating the Attention Mechanism in Transformer Models with a Fully Convolutional Network
The past decade has seen a remarkable surge in the adoption of deep learning techniques for computer vision (CV) tasks. Convolutional neural networks (CNNs)...
13 MIN READ

Jan 25, 2024
Announcing NVIDIA Metropolis Microservices for Jetson for Rapid Edge AI Development
Building vision AI applications for the edge often comes with notoriously long and costly development cycles. At the same time, quickly developing edge AI...
6 MIN READ
Data Center / Cloud

Apr 25, 2024
Announcing Confidential Computing General Access on NVIDIA H100 Tensor Core GPUs
NVIDIA launched the initial release of the Confidential Computing (CC) solution in private preview for early access in July 2023 through NVIDIA LaunchPad....
3 MIN READ

Apr 23, 2024
Democratizing AI Workflows with Union.ai and NVIDIA DGX Cloud
GPUs were initially specialized for rendering 3D graphics in video games, primarily to accelerate linear algebra calculations. Today, GPUs have become one of...
7 MIN READ

Apr 23, 2024
Webinar: Enhance LLMs with RAG and Accelerate Enterprise AI with Pure Storage and NVIDIA
Join Pure Storage and NVIDIA on April 25 to discover the benefits of enhancing LLMs with RAG for enterprise-scale generative AI applications.
1 MIN READ

Apr 22, 2024
Advancing Cell Segmentation and Morphology Analysis with NVIDIA AI Foundation Model VISTA-2D
Genomics researchers use different sequencing techniques to better understand biological systems, including single-cell and spatial omics. Unlike single-cell,...
7 MIN READ

Apr 22, 2024
Just Released: NVIDIA Modulus v24.04
Modulus v24.04 delivers an optimized CorrDiff model and Earth2Studio for exploring weather AI models.
1 MIN READ

Apr 22, 2024
Enhanced DU Performance and Workload Consolidation for 5G/6G with NVIDIA Aerial CUDA-Accelerated RAN
Aerial CUDA-Accelerated radio access network (RAN) enables acceleration of telco workloads, delivering new levels of spectral efficiency (SE) on a cloud-native...
14 MIN READ

Apr 19, 2024
Measuring the GPU Occupancy of Multi-stream Workloads
NVIDIA GPUs are becoming increasingly powerful with each new generation. This increase generally comes in two forms. Each streaming multi-processor (SM), the...
11 MIN READ

Apr 17, 2024
Advancing Medical Image Decoding with GPU-Accelerated nvImageCodec
This post delves into the capabilities of decoding DICOM medical images within AWS HealthImaging using the nvJPEG2000 library. We'll guide you through the...
16 MIN READ

Apr 10, 2024
How Generative AI is Empowering Climate Tech with NVIDIA Earth-2
In the context of global warming, NVIDIA Earth-2 has emerged as a pivotal platform for climate tech, generating actionable insights in the face of increasingly...
14 MIN READ

Apr 09, 2024
Next-Generation Live Media Apps on Repurposable Clusters with NVIDIA Holoscan for Media
NVIDIA Holoscan for Media is now available to all developers looking to build next-generation live media applications on fully repurposable clusters. ...
4 MIN READ

Mar 27, 2024
Efficient CUDA Debugging: Using NVIDIA Compute Sanitizer with NVIDIA Tools Extension and Creating Custom Tools
NVIDIA Compute Sanitizer is a powerful tool that can save you time and effort while improving the reliability and performance of your CUDA applications....
14 MIN READ
Mar 27, 2024
Develop Custom Enterprise Generative AI with NVIDIA NeMo
Generative AI is transforming computing, paving new avenues for humans to interact with computers in natural, intuitive ways. For enterprises, the prospect of...
14 MIN READ




