Linear Algebra
Apr 20, 2023
A Comprehensive Overview of Regression Evaluation Metrics
As a data scientist, evaluating machine learning model performance is a crucial aspect of your work. To do so effectively, you have a wide range of statistical...
17 MIN READ

Dec 05, 2017
CUTLASS: Fast Linear Algebra in CUDA C++
Update May 21, 2018: CUTLASS 1.0 is now available as Open Source software at the CUTLASS repository. CUTLASS 1.0 has changed substantially from our preview...
25 MIN READ
Oct 17, 2017
Programming Tensor Cores in CUDA 9
Tensor cores provide a huge boost to convolutions and matrix operations. Tensor cores are...
16 MIN READ

Feb 27, 2017
Pro Tip: cuBLAS Strided Batched Matrix Multiply
There’s a new computational workhorse in town. For decades, general matrix-matrix multiply—known as GEMM in Basic Linear Algebra Subroutines (BLAS)...
10 MIN READ
Jun 09, 2015
Graph Coloring: More Parallelism for Incomplete-LU Factorization
In this blog post I will briefly discuss the importance and simplicity of graph coloring and its application to one of the most common problems in sparse linear...
12 MIN READ

Apr 28, 2015
Parallel Direct Solvers with cuSOLVER: Batched QR
[Note: Lung Sheng Chien from NVIDIA also contributed to this post.] A key bottleneck for most science and engineering simulations is the solution of sparse...
15 MIN READ
Oct 23, 2014
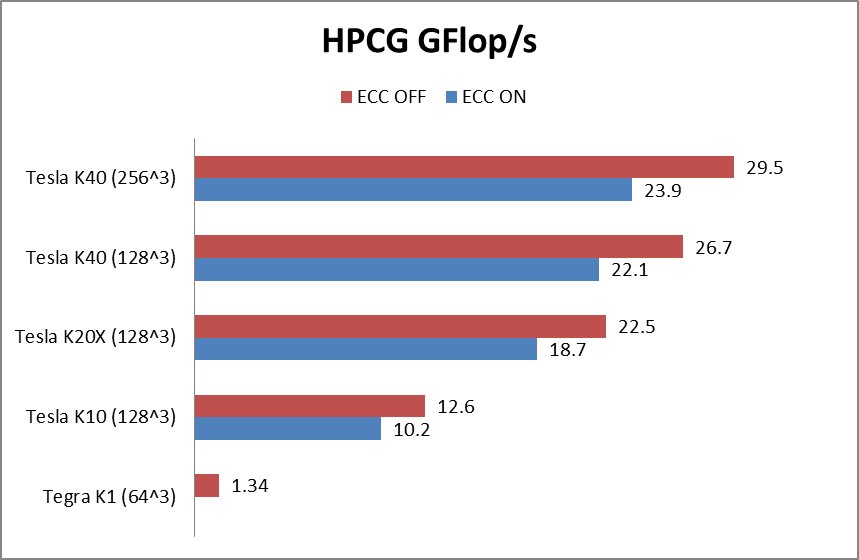
Optimizing the High Performance Conjugate Gradient Benchmark on GPUs
[This post was co-written by Everett Phillips and Massimiliano Fatica.] The High Performance Conjugate Gradient Benchmark (HPCG) is a new benchmark intended to...
11 MIN READ

Apr 29, 2014
CUDA Pro Tip: Fast and Robust Computation of Givens Rotations
A Givens rotation [1] represents a rotation in a plane represented by a matrix of the form $latex G(i, j, \theta) = \begin{bmatrix} 1 & \cdots & 0 &...
3 MIN READ