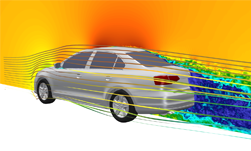
Many industries use Computational Fluid Dynamics (CFD) to predict fluid flow forces on products during the design phase, using only numerical methods. A famous example is Boeing’s 777 airliner, which was designed and built without the construction (or destruction) of a single model in a wind tunnel, an industry first. This approach dramatically reduces the cost of designing new products for which aerodynamics is a large part of the value add. Another good example is Formula 1 racing, where a fraction of a percentage point reduction in drag forces on the car body can make the difference between a winning or a losing season.
 Users of CFD models crave higher accuracy and faster run times. The key enabling algorithm for realistic models in CFD is Algebraic Multi-Grid (AMG). This algorithm allows solution times to scale linearly with the number of unknowns in the model; it can be applied to arbitrary geometries with highly refined and unstructured numerical meshes; and it can be run efficiently in parallel. Unfortunately, AMG is also very complex and requires specialty programming and mathematical skills, which are in short supply. Add in the need for GPU programming skills, and GPU-accelerated AMG seems a high mountain to climb. Existing GPU-accelerated AMG implementations (most notably the one in CUSP) are more proofs of concept than industrial strength solvers for real world CFD applications, and highly tuned multi-threaded and/or distributed CPU implementations can outperform them in many cases. Industrial CFD users had few options for GPU acceleration, so NVIDIA decided to do something about it.
Users of CFD models crave higher accuracy and faster run times. The key enabling algorithm for realistic models in CFD is Algebraic Multi-Grid (AMG). This algorithm allows solution times to scale linearly with the number of unknowns in the model; it can be applied to arbitrary geometries with highly refined and unstructured numerical meshes; and it can be run efficiently in parallel. Unfortunately, AMG is also very complex and requires specialty programming and mathematical skills, which are in short supply. Add in the need for GPU programming skills, and GPU-accelerated AMG seems a high mountain to climb. Existing GPU-accelerated AMG implementations (most notably the one in CUSP) are more proofs of concept than industrial strength solvers for real world CFD applications, and highly tuned multi-threaded and/or distributed CPU implementations can outperform them in many cases. Industrial CFD users had few options for GPU acceleration, so NVIDIA decided to do something about it.
NVIDIA partnered with ANSYS, provider of the leading CFD software Fluent to develop a high-performance, robust and scalable GPU-accelerated AMG library. We call the library AmgX (for AMG Accelerated). Fluent 15.0 uses AmgX as its default linear solver, and it takes advantage of a CUDA-enabled GPU when it detects one. AmgX can even use MPI to connect clusters of servers to solve very large problems that require dozens of GPUs. The aerodynamics problem in Figure 1 required 48 NVIDIA K40X GPUs, and involved 111million cells and over 440 million unknowns.

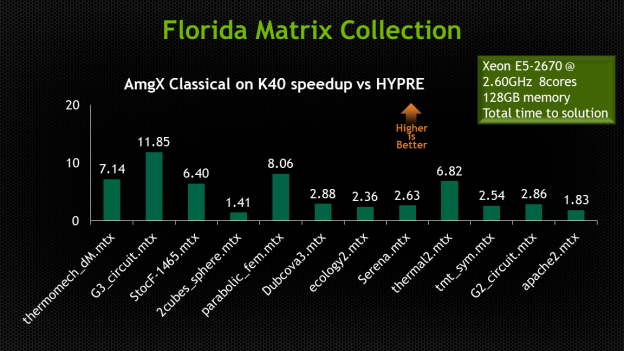
Here’s the best part: because AMG only needs the matrix and right hand side of the linear equations (A and b from Ax = b), it has applications far beyond aerodynamics models. We have tested it for reservoir simulations of oil and gas flows, models of flooding from tsunamis and hurricanes, heat transfer, circuit simulation, and mechanical stress models, and we see dramatic speedup over the highly tuned and multi-threaded HYPRE AMG package.
Batteries Included
AmgX delivers a complete toolkit for building specially tuned linear solvers, including:
- two forms of AMG: both ‘Classical’ and ‘Unsmoothed Aggregation’;
- Krylov iterative methods: GMRES, CG, BICGStab, with preconditioned and ‘flexible’ variants;
- simple iterative methods: Gauss-Seidel, Jacobi, Chebyshev, ILU0, ILU1;
- multi-colored versions which expose fine-grained parallelism;
- flexible configuration: all methods can appear as a solver, preconditioner or smoother, and can be nested and iterated to arbitrary levels;
- support for use in non-linear solvers: API methods for frequently changing matrix values, parallel and efficient setup.
Easy to Use
The AmgX API is straight C code, which links against C,C++ or Fortran programs, and requires no CUDA experience or knowledge to use. We designed a minimal API, focused on solving linear systems repeatedly. The matrix and vector inputs can be created on the host and copied to the device, or created directly on the GPU and passed to AmgX in place. AmgX works on Linux and Windows OSes, and supports applications using OpenMP, MPI or any mix of both. Following is a minimal code example of how AmgX would be used to solve a test system.
//One header #include “amgx_c.h” //Read config file AMGX_create_config(&cfg, cfgfile); //Create resources based on config AMGX_resources_create_simple(&res, cfg); //Create solver object, A,x,b, set precision AMGX_solver_create(&solver, res, mode, cfg); AMGX_matrix_create(&A,res,mode); AMGX_vector_create(&x,res,mode); AMGX_vector_create(&b,res,mode); //Read coefficients from a file AMGX_read_system(&A,&x,&b, matrixfile); //Setup and Solve AMGX_solver_setup(solver,A); AMGX_solver_solve(solver, b, x);
The configuration file is plain text, with a key-value system for specifying parameters and options. A typical config file might look like this:
solver(main)=FGMRES main:max_iters=100 main:convergence=RELATIVE_MAX main:tolerance=0.1 main:preconditioner(amg)=AMG amg:algorithm=AGGREGATION amg:selector=SIZE_8 amg:cycle=V amg:max_iters=1 amg:max_levels=10 amg:smoother(amg_smoother)=BLOCK_JACOBI amg:relaxation_factor= 0.75 amg:presweeps=1 amg:postsweeps=2 amg:coarsest_sweeps=4 determinism_flag=1
Integrating with Existing Solutions
We realized early on that users typically already have a working simulation or modeling code and probably even a multi-threaded solver, so we wanted to simplify the process of integrating AmgX with existing code. It’s common for a multi-threaded simulation to partition the problem into pieces and assign one piece to each CPU thread. AmgX provides a facility which we call consolidation that allows the user to maintain the multi-threaded decomposition they worked hard to create, and reassembles the pieces on the GPU for efficient solution.
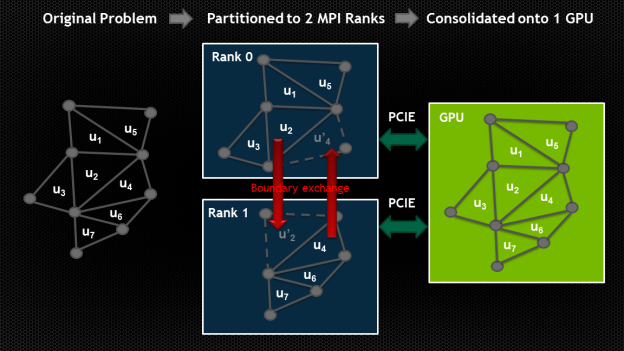
This allows the user to balance the work between several CPU cores and a single GPU, and find whatever ratio is best for their application without being locked into a fixed, arbitrary ratio by AmgX. If you already have working code, we don’t want to make you change anything beyond what is needed to connect to AmgX.
Benchmarks
We compared the AmgX solvers to the widely used HYPRE AMG package, using modern multi-core CPUs and our latest GPU hardware. We see the expected linear scaling as the number of unknowns increases. AmgX on an NVIDIA Tesla K40x GPU compares favorably to an 8-core CPU running HYPRE. We ran the miniFE ‘mini-app’ benchmark used by Sandia National Labs to compare parallel solvers using various hardware and software combinations. MiniFE exercises the data flow and algorithms used in a complex finite element model, including matrix assembly, partitioning and solution phases using a Conjugate Gradient (CG) solver. MiniFE is typically run for 200 iterations, and without AMG preconditioning it fails to converge. Using HYPRE or AmgX, miniFE converges to 1e-10 tolerance in less than 50 iterations. Both the Classical and Aggregation versions available in AmgX deliver a significant speedup for the miniFE application, and the speedup ratio increases with the problem size. At 6 million unknowns, we deliver an impressive 1.6x speedup.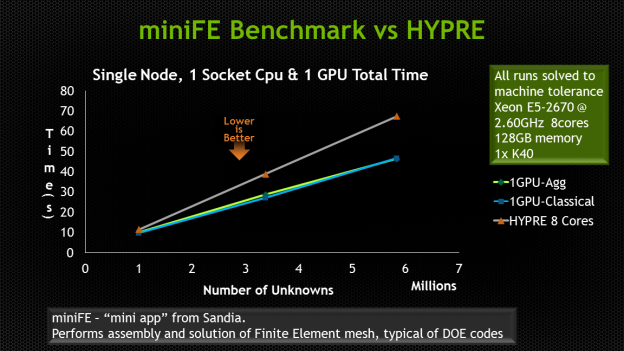
Try AmgX yourself!
AmgX is available free for academic and research use, with licenses available for commercial use. Just sign up for a registered CUDA developer account. Once your account is activated, log in and you will see a link to the AmgX download page. I recommend starting with the README, then compiling and running the examples included in the download directory.