In efficient parallel algorithms, threads cooperate and share data to perform collective computations. To share data, the threads must synchronize. The granularity of sharing varies from algorithm to algorithm, so thread synchronization should be flexible. Making synchronization an explicit part of the program ensures safety, maintainability, and modularity. CUDA 9 introduces Cooperative Groups, which aims to satisfy these needs by extending the CUDA programming model to allow kernels to dynamically organize groups of threads.
Historically, the CUDA programming model has provided a single, simple construct for synchronizing cooperating threads: a barrier across all threads of a thread block, as implemented with the __syncthreads() function. However, CUDA programmers often need to define and synchronize groups of threads smaller than thread blocks in order to enable greater performance, design flexibility, and software reuse in the form of “collective” group-wide function interfaces.
The Cooperative Groups programming model describes synchronization patterns both within and across CUDA thread blocks. It provides CUDA device code APIs for defining, partitioning, and synchronizing groups of threads. It also provides host-side APIs to launch grids whose threads are all guaranteed to be executing concurrently to enable synchronization across thread blocks. These primitives enable new patterns of cooperative parallelism within CUDA, including producer-consumer parallelism and global synchronization across the entire thread grid or even multiple GPUs.
The expression of groups as first-class program objects improves software composition: collective functions can take an explicit argument representing the group of participating threads. Consider a library function that imposes requirements on its caller. Explicit groups make these requirements explicit, reducing the chances of misusing the library function. Explicit groups and synchronization help make code less brittle, reduce restrictions on compiler optimization, and improve forward compatibility.
The Cooperative Groups programming model consists of the following elements:
- Data types representing groups of cooperating threads and their properties;
- Intrinsic groups defined by the CUDA launch API (e.g., thread blocks);
- Group partitioning operations;
- A group barrier synchronization operation;
- Group-specific collectives.
Cooperative Groups Fundamentals
At its simplest, Cooperative Groups is an API for defining and synchronizing groups of threads in a CUDA program. Much of the Cooperative Groups (in fact everything in this post) works on any CUDA-capable GPU compatible with CUDA 9. Specifically, that means Kepler and later GPUs (Compute Capability 3.0+).
To use Cooperative Groups, include its header file.
#include <cooperative_groups.h>
Cooperative Groups types and interfaces are defined in the cooperative_groups C++ namespace, so you can either prefix all names and functions with cooperative_groups::, or load the namespace or its types with using directives.
using namespace cooperative_groups; // or... using cooperative_groups::thread_group; // etc.
It’s not uncommon to alias it to something shorter. Assume the following namespace alias exists in the examples in this post.
namespace cg = cooperative_groups;
Code containing any intra-block Cooperative Groups functionality can be compiled in the normal way using nvcc (note that many of the examples in this post use C++11 features so you need to add the --std=c++11 option to the compilation command line).
Thread Groups
The fundamental type in Cooperative Groups is thread_group, which is a handle to a group of threads. The handle is only accessible to members of the group it represents. Thread groups expose a simple interface. You can get the size (total number of threads) of a group with the size() method:
unsigned size();
To find the index of the calling thread (between 0 and size()-1) within the group, use the thread_rank() method:
unsigned thread_rank();
Finally, you can check the validity of a group using the is_valid() method.
bool is_valid();
Thread Group Collective Operations
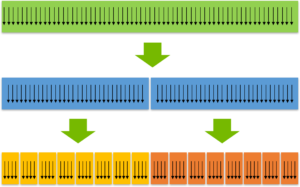
Thread groups provide the ability to perform collective operations among all threads in a group. Collective operations, or simply collectives, are operations that need to synchronize or otherwise communicate amongst a specified set of threads. Because of the need for synchronization, every thread that is identified as participating in a collective must make a matching call to that collective operation. The simplest collective is a barrier, which transfers no data and merely synchronizes the threads in the group. Synchronization is supported by all thread groups. As you’ll learn later in this post, some group types support other collectives.

You can synchronize a group by calling its collective sync() method, or by calling the cooperative_groups::sync() function. These perform barrier synchronization among all threads in the group (Figure 2).
g.sync(); // synchronize group g cg::synchronize(g); // an equivalent way to synchronize g
Here’s a simple example of a parallel reduction device function written using Cooperative Groups. When the threads of a group call it, they cooperatively compute the sum of the values passed by each thread in the group (through the val argument).
using namespace cooperative_groups;
__device__ int reduce_sum(thread_group g, int *temp, int val)
{
int lane = g.thread_rank();
// Each iteration halves the number of active threads
// Each thread adds its partial sum[i] to sum[lane+i]
for (int i = g.size() / 2; i > 0; i /= 2)
{
temp[lane] = val;
g.sync(); // wait for all threads to store
if(lane<i) val += temp[lane + i];
g.sync(); // wait for all threads to load
}
return val; // note: only thread 0 will return full sum
}
Now let’s look at how to create thread groups.
Thread Blocks
If you have programmed with CUDA before, you are familiar with thread blocks, the fundamental unit of parallelism in a CUDA program. Cooperative Groups introduces a new datatype, thread_block, to explicitly represent this concept within the kernel. An instance of thread_block is a handle to the group of threads in a CUDA thread block that you initialize as follows.
thread_block block = this_thread_block();
As with any CUDA program, every thread that executes that line has its own instance of the variable block. Threads with the same value of the CUDA built-in variable blockIdx are part of the same thread block group.
Synchronizing a thread_block group is much like calling __syncthreads(). The following lines of code all do the same thing (assuming all threads of the thread block reach them).
__syncthreads(); block.sync(); cg::synchronize(block); this_thread_block().sync(); cg::synchronize(this_thread_block());
The thread_block data type extends the thread_group interface with the following block-specific methods.
dim3 group_index(); // 3-dimensional block index within the grid dim3 thread_index(); // 3-dimensional thread index within the block
These are equivalent to CUDA’s blockIdx and threadIdx, respectively.
Here’s a simple kernel that uses the reduce_sum() device function to compute the sum of all values in an input array. It starts by computing many partial sums in parallel in thread_sum(), where each thread strides through the array computing a partial sum (and uses vector loads for higher memory access efficiency). The kernel then uses thread_block groups for cooperative summation, and atomicAdd() to combine the block sums.
__device__ int thread_sum(int *input, int n)
{
int sum = 0;
for(int i = blockIdx.x * blockDim.x + threadIdx.x;
i < n / 4;
i += blockDim.x * gridDim.x)
{
int4 in = ((int4*)input)[i];
sum += in.x + in.y + in.z + in.w;
}
return sum;
}
__global__ void sum_kernel_block(int *sum, int *input, int n)
{
int my_sum = thread_sum(input, n);
extern __shared__ int temp[];
auto g = this_thread_block();
int block_sum = reduce_sum(g, temp, my_sum);
if (g.thread_rank() == 0) atomicAdd(sum, block_sum);
}
We can launch this function to compute the sum of a 16M-element array like this.
int n = 1<<24; int blockSize = 256; int nBlocks = (n + blockSize - 1) / blockSize; int sharedBytes = blockSize * sizeof(int); int *sum, *data; cudaMallocManaged(&sum, sizeof(int)); cudaMallocManaged(&data, n * sizeof(int)); std::fill_n(data, n, 1); // initialize data cudaMemset(sum, 0, sizeof(int)); sum_kernel_block<<<nBlocks, blockSize, sharedBytes>>>(sum, data, n);
Partitioning Groups
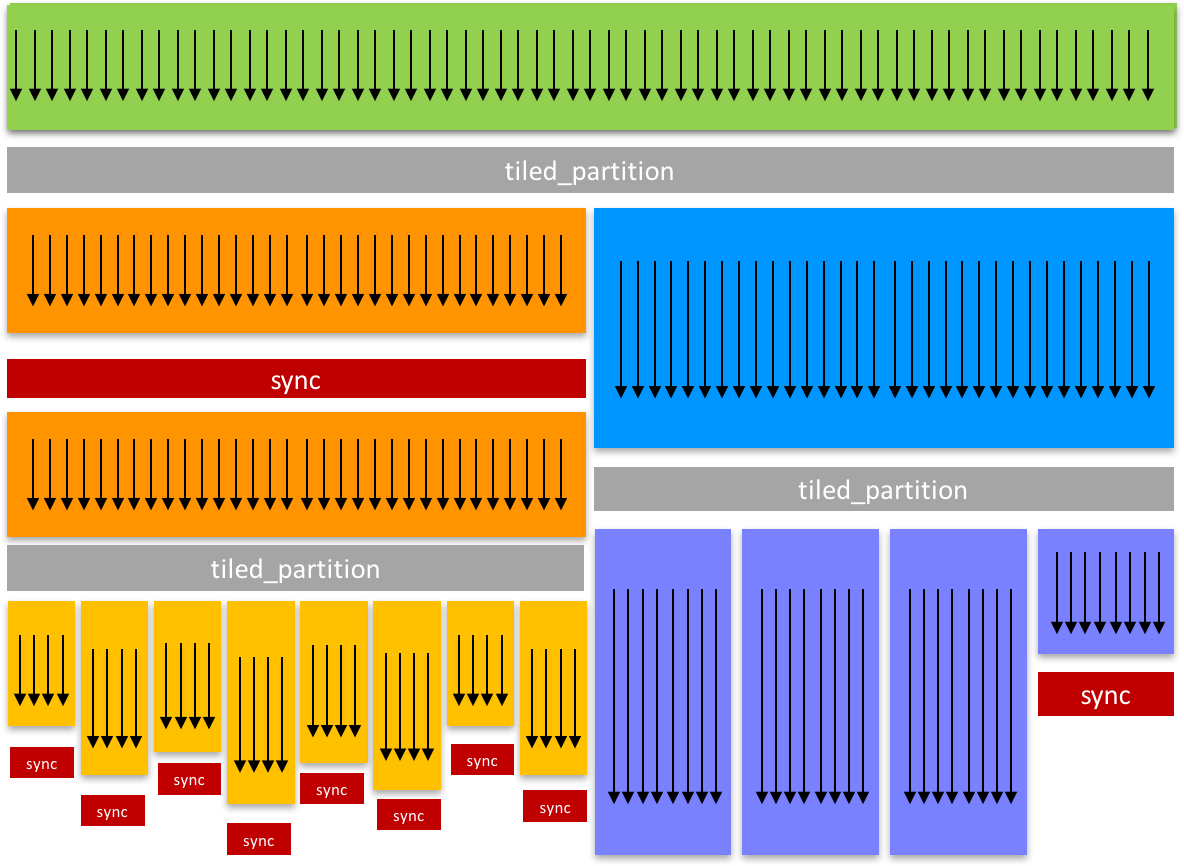
Cooperative Groups provides you the flexibility to create new groups by partitioning existing groups. This enables cooperation and synchronization at a finer granularity. The cg::tiled_partition() function partitions a thread block into multiple “tiles”. Here’s an example that partitions each whole thread block into tiles of 32 threads.
thread_group tile32 = cg::tiled_partition(this_thread_block(), 32);
Each thread that executes the partition will get a handle (in tile32) to one 32-thread group. 32 is a common choice, because it corresponds to a warp: the unit of threads that are scheduled concurrently on a GPU streaming multiprocessor (SM).
Here’s another example where we partition into groups of four threads.
thread_group tile4 = tiled_partition(tile32, 4);
The thread_group objects returned by tiled_partition() are just like any thread group. So, for example, we can do things like this:
if (tile4.thread_rank()==0)
printf("Hello from tile4 rank 0: %d\n",
this_thread_block().thread_rank());
Every fourth thread will print, as in the following.
Hello from tile4 rank 0: 0 Hello from tile4 rank 0: 4 Hello from tile4 rank 0: 8 Hello from tile4 rank 0: 12 ...
Modularity
The real power of Cooperative Groups lies in the modularity that arises when you can pass a group as an explicit parameter to a function and depend on a consistent interface across a variety of thread group sizes. This makes it harder to inadvertently cause race conditions and deadlock situations by making invalid assumptions about which threads will call a function concurrently. Let’s me show you an example.
__device__ int sum(int *x, int n)
{
...
__syncthreads();
...
return total;
}
__global__ void parallel_kernel(float *x, int n)
{
if (threadIdx.x < blockDim.x / 2)
sum(x, count); // error: half of threads in block skip
// __syncthreads() => deadlock
}
In the preceding code example, a portion of the threads of each block call sum(), which calls __syncthreads(). Since not all threads in the block reach the __syncthreads(), there is a deadlock situation, since __syncthreads() invokes a barrier which waits until all threads of the block reach it. Without knowing the details of the implementation of a library function like sum(), this is an easy mistake to make.
The following code uses Cooperative Groups to require that a thread block group be passed into the call. This makes that mistake much harder to make.
// Now much clearer that a whole thread block is expected to call
__device__ int sum(thread_block block, int *x, int n)
{
...
block.sync();
...
return total;
}
__global__ void parallel_kernel(float *x, int n)
{
sum(this_thread_block(), x, count); // no divergence around call
}
In the first (incorrect) example, the caller wanted to use fewer threads to compute sum(). The modularity enabled by Cooperative Groups means that we can apply the same reduction function to a variety of group sizes. Here’s another version of our sum kernel that uses tiles of 32 threads instead of whole thread blocks. Each tile does a parallel reduction—using the same reduce_sum() function as before—and then atomically adds its result to the total.
__global__ void sum_kernel_32(int *sum, int *input, int n)
{
int my_sum = thread_sum(input, n);
extern __shared__ int temp[];
auto g = this_thread_block();
auto tileIdx = g.thread_rank() / 32;
int* t = &temp[32 * tileIdx];
auto tile32 = tiled_partition(g, 32);
int tile_sum = reduce_sum(tile32, t, my_sum);
if (tile32.thread_rank() == 0) atomicAdd(sum, tile_sum);
}
Optimizing for the GPU Warp Size
Cooperative Groups provides an alternative version of cg::tiled_partition() that takes the tile size as a template parameter, returning a statically sized group called a thread_block_tile. Knowing the tile size at compile time provides the opportunity for better optimization. Here are two static tiled partitions that match the two examples given previously.
thread_block_tile<32> tile32 = tiled_partition<32>(this_thread_block()); thread_block_tile<4> tile4 = tiled_partition<4> (this_thread_block());
We can use this to slightly optimize our tiled reduction so that when passed a statically sized thread_block_tile the inner loop will be unrolled.
template <typename group_t>
__device__ int reduce_sum(group_t g, int *temp, int val)
{
int lane = g.thread_rank();
// Each iteration halves the number of active threads
// Each thread adds its partial sum[i] to sum[lane+i]
#pragma unroll
for (int i = g.size() / 2; i > 0; i /= 2)
{
temp[lane] = val;
g.sync(); // wait for all threads to store
if (lane < i) val += temp[lane + i];
g.sync(); // wait for all threads to load
}
return val; // note: only thread 0 will return full sum
}
Also, when the tile size matches the hardware warp size, the compiler can elide the synchronization while still ensuring correct memory instruction ordering to avoid race conditions. Intentionally removing synchronizations is an unsafe technique (known as implicit warp synchronous programming) that expert CUDA programmers have often used to achieve higher performance for warp-level cooperative operations. Always explicitly synchronize your thread groups, because implicitly synchronized programs have race conditions.
For parallel reduction, which is bandwidth bound, this code is not significantly faster on recent architectures than the non-static tiled_partition version. But it demonstrates the mechanics of statically sized tiles which can be beneficial in more computationally intensive uses.
Warp-Level Collectives
Thread Block Tiles also provide an API for the following warp-level collective functions:
.shfl()
.shfl_down()
.shfl_up()
.shfl_xor()
.any()
.all()
.ballot()
.match_any()
.match_all()
These operations are all primitive operations provided by NVIDIA GPUs starting with the Kepler architecture (Compute Capability 3.x), except for match_any() and match_all(), which are new in the Volta architecture (Compute Capability 7.x).
Using thread_block_tile::shfl_down() to simplify our warp-level reduction does benefit our code: it simplifies it and eliminates the need for shared memory.
template <int tile_sz>
__device__ int reduce_sum_tile_shfl(thread_block_tile<tile_sz> g, int val)
{
// Each iteration halves the number of active threads
// Each thread adds its partial sum[i] to sum[lane+i]
for (int i = g.size() / 2; i > 0; i /= 2) {
val += g.shfl_down(val, i);
}
return val; // note: only thread 0 will return full sum
}
template<int tile_sz>
__global__ void sum_kernel_tile_shfl(int *sum, int *input, int n)
{
int my_sum = thread_sum(input, n);
auto tile = tiled_partition<tile_sz>(this_thread_block());
int tile_sum = reduce_sum_tile_shfl<tile_sz>(tile, my_sum);
if (tile.thread_rank() == 0) atomicAdd(sum, tile_sum);
}
Discovering Thread Concurrency
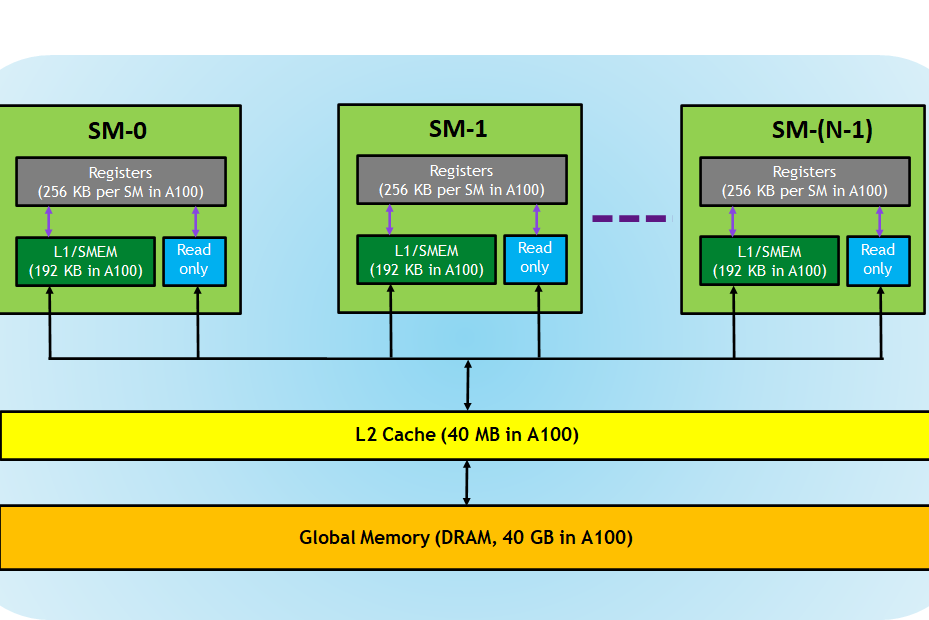
In the GPU’s SIMT (Single Instruction Multiple Thread) architecture, the GPU streaming multiprocessors (SM) execute thread instructions in groups of 32 called warps. The threads in a SIMT warp are all of the same type and begin at the same program address, but they are free to branch and execute independently. At each instruction issue time, the instruction unit selects a warp that is ready to execute and issues its next instruction to the warp’s active threads. The instruction unit applies an active mask to the warp to ensure that only threads that are active issue the instruction. Individual threads in a warp may be inactive due to independent branching in the program.
Thus, when data-dependent conditional branches in the code cause threads within a warp to diverge, the SM disables threads that don’t take the branch. The threads that remain active on the path are referred to as coalesced.
Cooperative Groups provides the function coalesced_threads() to create a group comprising all coalesced threads:
coalesced_group active = coalesced_threads();
As an example, consider the following thread that creates a coalesced_group inside a divergent branch taken only by odd-numbered threads. Odd-numbered threads within a warp will be part of the same coalesced_group, and thus they can be synchronized by calling active.sync().
auto block = this_thread_block();
if (block.thread_rank() % 2) {
coalesced_group active = coalesced_threads();
...
active.sync();
}
Keep in mind that since threads from different warps are never coalesced, the largest group that coalesced_threads() can return is a full warp.
It’s common to need to work with the current active set of threads, without making assumptions about which threads are present. This is necessary to ensure modularity of utility functions that may be called in different situations but which still want to coordinate the activities of whatever threads happen to be active.
A good example is “warp-aggregated atomics”. In warp aggregation, the threads of a warp first compute a total increment among themselves, and then elect a single thread to atomically add the increment to a global counter. This aggregation reduces the number of atomics performed by up to the number of threads in a warp (up to 32x on current GPUs), and can dramatically improve performance. Moreover, it can be used as a drop-in replacement for atomicAdd(). You can see the full details of warp-aggregated atomics in this NVIDIA Developer Blog post.
The key to correct operation of warp aggregation is in electing a thread from the warp to perform the atomic add. To enable use inside divergent branches, warp aggregation can’t just pick thread zero of the warp because it might be inactive in the current branch. Instead, as the blog post explains, warp intrinsics can be used to elect the first active thread in the warp.
The Cooperative Groups coalesced_group type makes this trivial, since its thread_rank() method ranks only threads that are part of the group. This enables a simple implementation of warp-aggregated atomics that is robust and safe to use on any GPU architecture. The coalesced_group type also supports warp intrinsics like shfl(), use in the following code to broadcast to all threads in the group.
__device__
int atomicAggInc(int *ptr)
{
cg::coalesced_group g = cg::coalesced_threads();
int prev;
// elect the first active thread to perform atomic add
if (g.thread_rank() == 0) {
prev = atomicAdd(ptr, g.size());
}
// broadcast previous value within the warp
// and add each active thread’s rank to it
prev = g.thread_rank() + g.shfl(prev, 0);
return prev;
}
Get Started with Cooperative Groups
We hope that after reading this introduction you are as excited as we are about the possibilities of flexible and explicit groups of cooperating threads for sophisticated GPU algorithms. To get started with Cooperative Groups today, download the CUDA Toolkit version 9 or higher from https://developer.nvidia.com/cuda-toolkit. The toolkit includes various examples that use Cooperative Groups.

But we haven’t covered everything yet! New features in Pascal and Volta GPUs help Cooperative Groups go farther, by enabling creation and synchronization of thread groups that span an entire kernel launch running on one or even multiple GPUs. In a follow-up post we plan to cover the grid_group and multi_grid_group types and the cudaLaunchCooperative* APIs that enable them. Stay tuned.