Note: This post has been updated (November 2017) for CUDA 9 and the latest GPUs. The NVCC compiler now performs warp aggregation for atomics automatically in many cases, so you can get higher performance with no extra effort. In fact, the code generated by the compiler is actually faster than the manually-written warp aggregation code. This post is mainly intended for those who want to learn how it works, and apply a similar technique to other problems.
In this post, I’ll introduce warp-aggregated atomics, a useful technique to improve performance when many threads atomically add to a single counter. In warp aggregation, the threads of a warp first compute a total increment among themselves, and then elect a single thread to atomically add the increment to a global counter. This aggregation reduces the number of atomics performed by up to the number of threads in a warp (up to 32x on current GPUs), and can dramatically improve performance. Moreover, in many typical cases, you can implement warp aggregation as a drop-in replacement for standard atomic operations, so it is useful as a simple way to improve performance of complex applications.
Problem: Filtering by a Predicate
Consider the following filtering problem: I have a source array, src, containing n elements, and a predicate, and I need to copy all elements of src satisfying the predicate into the destination array, dst. For the sake of simplicity, assume that dst has length of at least n and that the order of elements in the dst array does not matter. For this example, I assume that the array elements are integers, and the predicate is true if and only if the element is positive. Here is a sample CPU implementation of filtering.
int filter(int *dst, const int *src, int n) {
int nres = 0;
for (int i = 0; i < n; i++)
if (src[i] > 0)
dst[nres++] = src[i];
// return the number of elements copied
return nres;
}
Filtering, also known as stream compaction, is a common operation, and it is a part of the standard libraries of many programming languages, where it goes under a variety of names, including grep, copy_if, select, FindAll and so on. It is also very often implemented simply as a loop, as it may be very tightly integrated with the surrounding code.
Solutions with Global and Shared Memory
Now, what if I want to implement filtering on a GPU, and process the elements of the array src in parallel? A straightforward approach is to use a single global counter and atomically increment it for each new element written int the dst array. A GPU implementation of this may look as follows.
__global__
void filter_k(int *dst, int *nres, const int *src, int n) {
int i = threadIdx.x + blockIdx.x * blockDim.x;
if(i < n && src[i] > 0)
dst[atomicAdd(nres, 1)] = src[i];
}
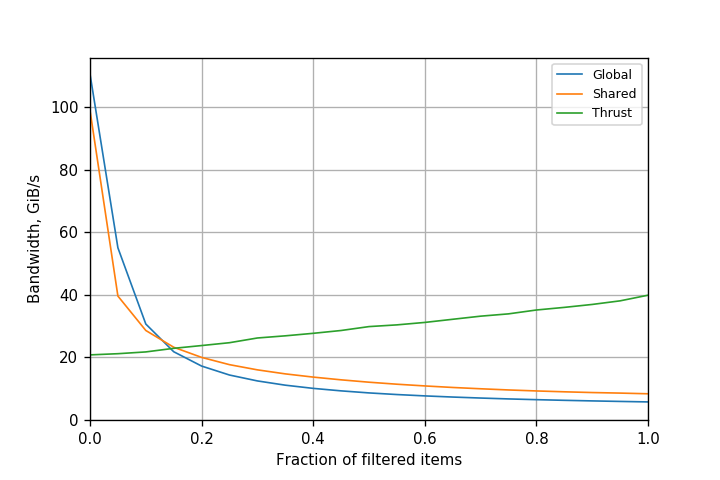
The main problem with this implementation is that all threads in the grid that read positive elements from src increment a single counter, nres. Depending on the number of positive elements, this may be a very large number of threads. Therefore, the degree of collisions for atomicAdd() is high, which limits performance. You can see this in Figure 1, which plots the kernel bandwidth (counting both reads and writes, but not atomics) achieved on a Kepler K80 GPU when processing 100 million (100*220) elements.
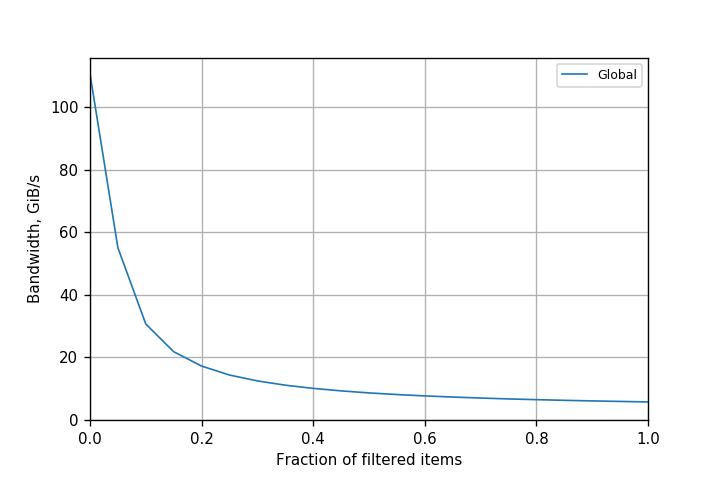
The bandwidth is inversely proportional to the number of atomics executed, or the fraction of positive elements in the array. While performance is acceptable (about 55 GiB/s) for a 5% fraction, it drops drastically when more elements pass the filter, to just around 8 GiB/s for a 50% fraction. Atomic operations are clearly a bottleneck, and need to be removed or reduced to increase application performance.
One way to improve filtering performance is to use shared memory atomics. This increases the speed of each operation, and reduces the degree of collisions, as the counter is only shared between threads in a single block. With this approach, we only need one global atomicAdd() per thread block. Here is a kernel implemented with this approach.
__global__
void filter_shared_k(int *dst, int *nres, const int* src, int n) {
__shared__ int l_n;
int i = blockIdx.x * (NPER_THREAD * BS) + threadIdx.x;
for (int iter = 0; iter < NPER_THREAD; iter++) {
// zero the counter
if (threadIdx.x == 0)
l_n = 0;
__syncthreads();
// get the value, evaluate the predicate, and
// increment the counter if needed
int d, pos;
if(i < n) {
d = src[i];
if(d > 0)
pos = atomicAdd(&l_n, 1);
}
__syncthreads();
// leader increments the global counter
if(threadIdx.x == 0)
l_n = atomicAdd(nres, l_n);
__syncthreads();
// threads with true predicates write their elements
if(i < n && d > 0) {
pos += l_n; // increment local pos by global counter
dst[pos] = d;
}
__syncthreads();
i += BS;
}
}
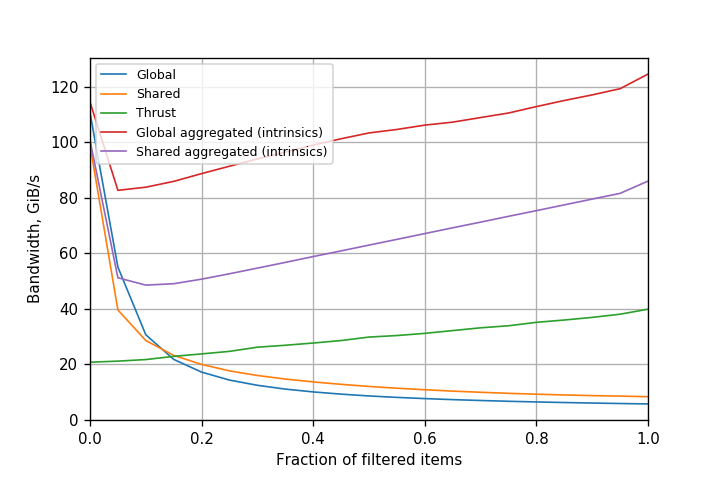
Another approach is to first use a parallel prefix sum to compute the output index of each element. Thrust’s copy_if() function uses an optimized version of this approach. Performance of both approaches for Kepler K80 is presented in Figure 2. Though shared memory atomics improve filtering performance, it still stays within 1.5x of the original approach. Atomics are still a bottleneck, as the number of operations hasn’t changed. Thrust is better than both approaches for high filtering fractions, but incurs large upfront costs which are not amortized for small filtering fractions.
It is important to note that the comparison to Thrust is not apples-to-apples, because Thrust implements a stable filter: it preserves the relative order of the input elements in the output. This is a result of using prefix sum to implement it, but it is more expensive as a result. If we don’t need a stable filter, then a purely atomic approach is simpler and performs less work.
Warp-Aggregated Atomics
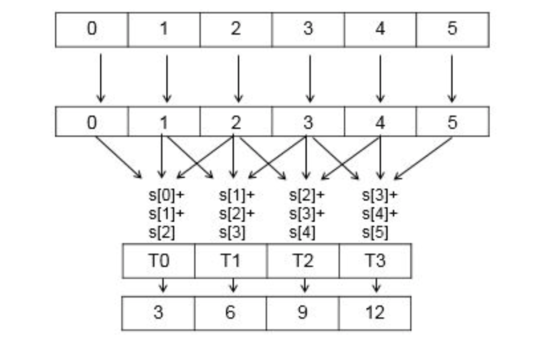
Warp aggregation is the process of combining atomic operations from multiple threads in a warp into a single atomic. This approach is orthogonal to using shared memory: the type of the atomics remains the same, but we use fewer of them. With warp aggregation, we replace atomic operations with the following steps.
- Threads in the warp elect a leader thread.
- Threads in the warp compute the total atomic increment for the warp.
- The leader thread performs an atomic add to compute the offset for the warp.
- The leader thread broadcasts the offset to all other threads in the warp.
- Each thread adds its own index within the warp to the warp offset to get its position in the output array.
Starting from CUDA 9.0, there are two APIs available to implement this: Cooperative Groups, an extension to the CUDA programming model for managing groups of cooperating threads, and warp-synchronous primitive functions.
After performing a warp-aggregated atomic, each thread proceeds as in the original code, and writes its value to its position in the dst array. Let’s now consider each of the steps in detail.
Step 1: Leader Election
In filtering, it’s possible to reorganize the code so that all threads are active. However, in other cases, atomics can occur within nested conditionals where some threads may be inactive. Generally, the approach should assume that only some threads are active, so I need a group made up of all active threads.
To use Cooperative Groups, include the header file and use the cooperative_groups namespace.
#include <cooperative_groups.h> using namespace cooperative_groups;
Create a group of all currently coalesced threads.
auto g = coalesced_threads();
Getting the thread rank is easy with Cooperative Groups: call g.thread_rank(). The thread with rank 0 will be the leader.
If you prefer to use primitive functions, start with __activemask().
unsigned int active = __activemask();
(An older approach is to use __ballot(1). This works with CUDA 8, but is deprecated starting with CUDA 9.)
Then elect a leader. Threads within a warp are called lanes; the simplest way to elect a leader is to use the active lane with the lowest number. The __ffs() primitive returns the 1-based index of the lowest set bit, so subtract 1 to get a 0-based index.
int leader = __ffs(active) - 1;
Step 2: Computing the Total Increment
For the filtering example, each thread with a true predicate increments the counter by 1. The total increment for the warp is equal to the number of active lanes (I don’t consider here the case of increments that vary across lanes). This is trivial with Cooperative Groups: g.size() returns the number of threads in the group.
If you prefer to use primitive functions, you can compute the total increment as the number of bits set in the mask returned by __activemask(). For this, use the __popc(int v) intrinsic, which returns the number of bits set in the binary representation of integer v. The following code computes the total increment.
int change = __popc(active);
Step 3: Performing the Atomic Add
Only the leader thread (lane 0) performs the atomic operation. With Cooperative Groups, just check if thread_rank() returns 0, like this.
int warp_res; if(g.thread_rank() == 0) warp_res = atomicAdd(ctr, g.size());
If you prefer to use primitive functions, you must compute the rank of each lane using __lanemask_lt(), which returns the mask of all lanes (including inactive ones) with ID less than the current lane. You can then compute the rank by ANDing this mask with the active lane mask, and counting the number of bits set.
unsigned int rank = __popc(active & __lanemask_lt()); int warp_old; if(rank == 0) warp_old = atomicAdd(ctr, change); // ctr is the pointer to the counter
Step 4: Broadcasting the Result
In this step, the leader thread broadcasts the result of the atomicAdd() to other lanes in the warp. We can do this by using the shuffle operation across the active lanes.
With Cooperative Groups, you can broadcast the result using g.shfl(warp_res, 0). The 0 is the index of the leader thread, which works since only active threads are part of the group (because it was created using coalesced_threads()).
If you prefer to use primitive functions, call __shfl_sync(), which has the following signature, where T is a 32- or 64-bit integer or floating-point type.
T __shfl_sync(unsigned int mask, T var, int srcLane, int width=warpSize);
shfl_sync() returns the value var held by the thread whose ID is given by srcLane. mask is the mask of threads participating in the call. All non-exited threads for which the mask bit is 1 must execute the same intrinsic with the same mask, or the result is undefined. width must be a power of two less than or equal to the warp size. The warp is broken into groups of that size, and srcLane refers to the lane number within the group. If srcLane is outside of range [0:width-1] (including both ends), then srcLane modulo width gives the lane number.
The following code uses __shfl_sync() to broadcast the result.
warp_res = __shfl_sync(active, warp_res, leader);
CUDA 8 and earlier implementations used __shfl(), which is deprecated starting with CUDA 9.
Step 5: Computing the Result for Each Lane
The last step computes the output position for each lane, by adding the broadcast counter value for the warp to the lane’s rank among the active lanes.
In Cooperative Groups:
return g.shfl(warp_res, 0) + g.thread_rank();
With primitive functions:
return warp_res + rank;
We can now join the pieces of the code for steps 1-5 to obtain the full warp-aggregated version of the increment function.
With Cooperative Groups, the code is concise and clear.
__device__ int atomicAggInc(int *ctr) {
auto g = coalesced_threads();
int warp_res;
if(g.thread_rank() == 0)
warp_res = atomicAdd(ctr, g.size());
return g.shfl(warp_res, 0) + g.thread_rank();
}
With primitive functions, the code is more complex.
__device__ int atomicAggInc(int *ctr) {
unsigned int active = __activemask();
int leader = __ffs(active) - 1;
int change = __popc(active);
unsigned int rank = __popc(active & __lanemask_lt());
int warp_res;
if(rank == 0)
warp_res = atomicAdd(ctr, change);
warp_res = __shfl_sync(active, warp_res, leader);
return warp_res + rank;
}
Performance Comparison
The warp-aggregated atomic increment function is a drop-in replacement for atomicAdd(ctr, 1) where ctr is the same across all threads of a warp. Therefore, we can rewrite GPU filtering using atomicAggInc() as follows.
__global__ void filter_k(int *dst, const int *src, int n) {
int i = threadIdx.x + blockIdx.x * blockDim.x;
if(i >= n)
return;
if(src[i] > 0)
dst[atomicAggInc(nres)] = src[i];
}
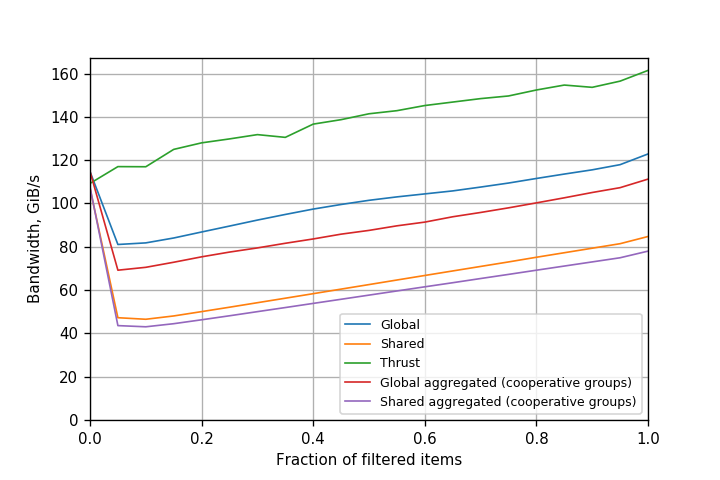
Note that though we defined warp aggregation with global atomics in mind, nothing precludes doing the same for shared memory atomics. In fact, the atomicAggInc(int *ctr) function defined above works if ctr is a pointer to shared memory. Warp aggregation can thus also be used to accelerate filtering with shared memory. Figure 3 shows a performance comparison of different variants of filtering with and without warp aggregation for a Kepler GPU.
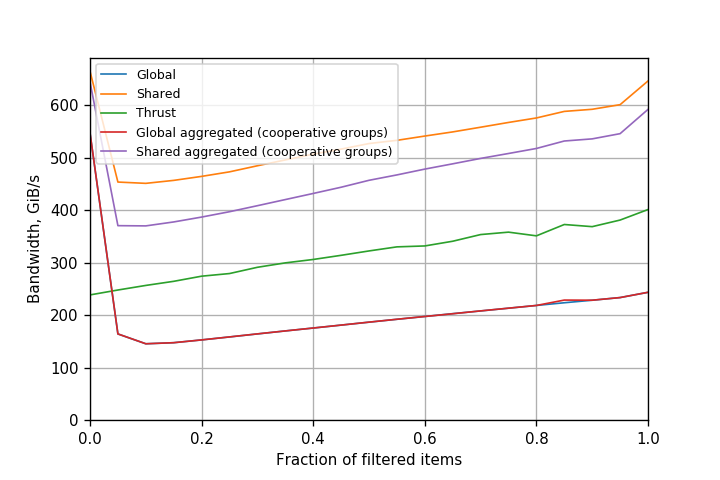
For Kepler GPUs, the version with warp-aggregated global atomics is the clear winner. It always provides more than 80 GiB/s bandwidth, and the bandwidth actually increases with the fraction of elements that successfully pass through the filter. This also indicates that atomics are no longer a significant bottleneck. Compared to global atomics, performance improves up to 21x. Performance of a simple copy operation on the same GPU is around 190 GiB/s. We can thus say that the performance of filtering with warp-aggregated atomics is comparable to that of a simple copy operation. This also means that filtering can now be used in performance-critical portions of the code. Also note that shared memory atomics (with warp aggregation) are actually slower than warp-aggregated atomics. This indicates that warp aggregation already does a very good job, and using shared memory on Kepler brings no benefit and only introduces additional overhead.
Since warp-aggregated atomics can be used as a drop-in replacement for normal atomics in certain cases, it is not a surprise that the compiler now performs this optimization automatically in many cases now. In fact, the compiler does the optimization for post-Kepler GPUs starting with CUDA 7.5, and in CUDA 9, it also does it for Kepler GPUs. Therefore, earlier comparisons were performed with CUDA 8 on Kepler, where warp-aggregated atomics were not yet inserted automatically.
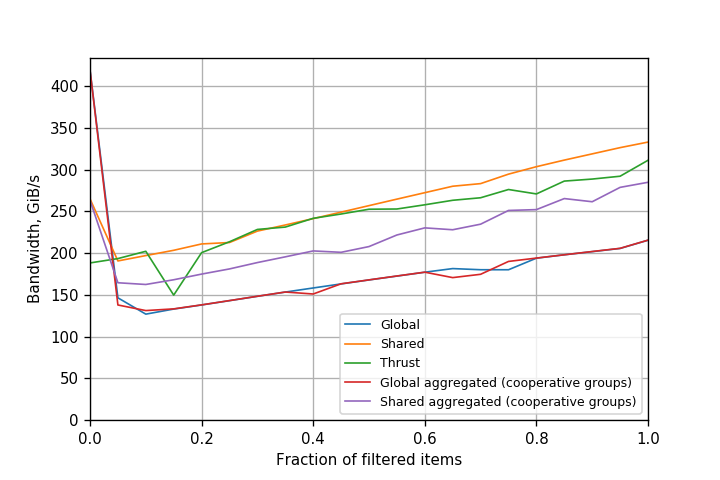
Figures 4, 5 and 6 show the comparison for Kepler, Pascal and Volta with CUDA 9. The performance of simple atomicAdd() is similar to that of warp-aggregated atomics.
Conclusion
Warp aggregation of atomics is a useful technique to improve performance of applications that perform many operations on a small number of counters. In this post we applied warp aggregation to filtering, and obtained more than an order-of-magnitude performance improvement for Kepler with CUDA 8. In fact, the technique turns out to be so useful that it is now implemented in the NVCC compiler, and you get warp aggregation in many cases by default with no additional effort required.
Warp-aggregated atomics are by no means limited to filtering; you can use it for many other applications which make use of atomic operations.