Update May 21, 2018: CUTLASS 1.0 is now available as Open Source software at the CUTLASS repository. CUTLASS 1.0 has changed substantially from our preview release described in the blog post below. We have decomposed the structure of the GEMM computation into deeper, structured primitives for loading data, computing predicate masks, streaming data at each level of the GEMM hierarchy, and updating the output matrix. CUTLASS 1.0 is described in the Doxygen documentation and our talk at the GPU Technology Conference 2018.
Matrix multiplication is a key computation within many scientific applications, particularly those in deep learning. Many operations in modern deep neural networks are either defined as matrix multiplications or can be cast as such.
As an example, the NVIDIA cuDNN library implements convolutions for neural networks using various flavors of matrix multiplication, such as the classical formulation of direct convolution as a matrix product between image-to-column and filter datasets [1]. Matrix multiplication is also the core routine when computing convolutions based on Fast Fourier Transforms (FFT) [2] or the Winograd approach [3].
When constructing cuDNN, we began with our high-performance implementations of general matrix multiplication (GEMM) in the cuBLAS library, supplementing and tailoring them to efficiently compute convolution. Today, our ability to adapt these GEMM strategies and algorithms is critical to delivering the best performance for many different problems and applications within deep learning.
With CUTLASS, we would like to give everyone the techniques and structures they need to develop new algorithms in CUDA C++ using high-performance GEMM constructs as building blocks. The flexible and efficient application of dense linear algebra is crucial within deep learning and the broader GPU computing ecosystem.
Introducing CUTLASS
Today, we are introducing a preview of CUTLASS (CUDA Templates for Linear Algebra Subroutines), a collection of CUDA C++ templates and abstractions for implementing high-performance GEMM computations at all levels and scales within CUDA kernels. Unlike other templated GPU libraries for dense linear algebra (e.g., the MAGMA library [4]), the purpose of CUTLASS is to decompose the “moving parts” of GEMM into fundamental components abstracted by C++ template classes, allowing programmers to easily customize and specialize them within their own CUDA kernels. We are releasing our CUTLASS source code on GitHub as an initial exposition of CUDA GEMM techniques that will evolve into a template library API.
Our CUTLASS primitives include extensive support for mixed-precision computations, providing specialized data-movement and multiply-accumulate abstractions for handling 8-bit integer, half-precision floating point (FP16), single-precision floating point (FP32), and double-precision floating point (FP64) types. One of the most exciting features of CUTLASS is an implementation of matrix multiplication that runs on the new Tensor Cores in the Volta architecture using the WMMA API. Tesla V100’s Tensor Cores are programmable matrix-multiply-and-accumulate units that can deliver up to 125 Tensor TFLOP/s with high efficiency.
Efficient Matrix Multiplication on GPUs
GEMM computes C = alpha A * B + beta C, where A, B, and C are matrices. A is an M-by-K matrix, B is a K-by-N matrix, and C is an M-by-N matrix. For simplicity, let us assume scalars alpha=beta=1 in the following examples. Later, we will show how to implement custom element-wise operations with CUTLASS supporting arbitrary scaling functions.
The simplest implementation consists of three nested loops:
for (int i = 0; i < M; ++i)
for (int j = 0; j < N; ++j)
for (int k = 0; k < K; ++k)
C[i][j] += A[i][k] * B[k][j];
The element of C at position (i, j) is the K-element dot product of the i-th row of A and the j-th column of B. Ideally, performance should be limited by the arithmetic throughput of the processor. Indeed, for large square matrices where M=N=K, the number of math operations in a product of matrices is O(N3) while the amount of data needed is O(N2), yielding a compute intensity on the order of N. However, taking advantage of the theoretical compute intensity requires reusing every element O(N) times. Unfortunately, the above “inner product” algorithm depends on holding a large working set in fast on-chip caches, which results in thrashing as M, N, and K grow.
A better formulation permutes the loop nest by structuring the loop over the K dimension as the outermost loop. This form of the computation loads a column of A and a row of B once, computes its outer product, and accumulates the result of this outer product in the matrix C. Afterward, this column of A and row of B are never used again.
for (int k = 0; k < K; ++k) // K dimension now outer-most loop
for (int i = 0; i < M; ++i)
for (int j = 0; j < N; ++j)
C[i][j] += A[i][k] * B[k][j];
One concern with this approach is that it requires all M-by-N elements of C to be live to store the results of each multiply-accumulate instruction, ideally in memory that can be written as fast as the multiply-accumulate instruction can be computed. We can reduce the working set size of C by partitioning it into tiles of size Mtile-by-Ntile that are guaranteed to fit into on-chip memory. Then we apply the “outer product” formulation to each tile. This leads to the following loop nest.
for (int m = 0; m < M; m += Mtile) // iterate over M dimension
for (int n = 0; n < N; n += Ntile) // iterate over N dimension
for (int k = 0; k < K; ++k)
for (int i = 0; i < Mtile; ++i) // compute one tile
for (int j = 0; j < Ntile; ++j) {
int row = m + i;
int col = n + j;
C[row][col] += A[row][k] * B[k][col];
}
For each tile of C, tiles of A and B are fetched exactly once, which achieves O(N) compute intensity. The size of each tile of C may be chosen to match the capacity of the L1 cache or registers of the target processor, and the outer loops of the nest may be trivially parallelized. This is a great improvement!
Further restructuring offers additional opportunities to exploit both locality and parallelism. Rather than exclusively accumulate vector outer products, we can accumulate the products of matrices by stepping through the K dimension in blocks. We refer to this concept generally as accumulating matrix products.
Hierarchical GEMM Structure
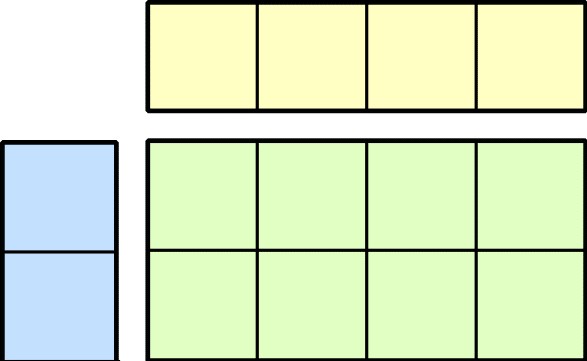
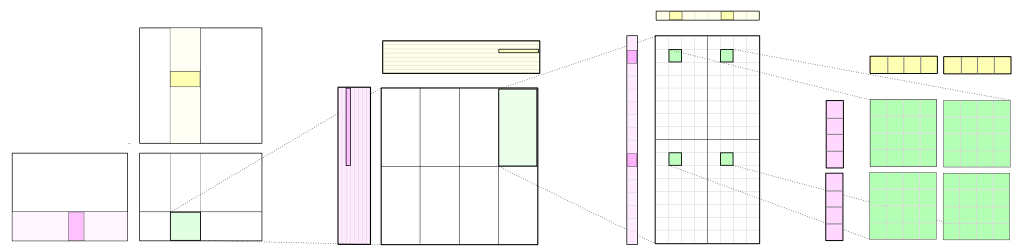
CUTLASS applies the tiling structure to implement GEMM efficiently for GPUs by decomposing the computation into a hierarchy of thread block tiles, warp tiles, and thread tiles and applying the strategy of accumulating matrix products. This hierarchy closely mirrors the NVIDIA CUDA programming model, as Figure 1 shows. Here, you can see data movement from global memory to shared memory (matrix to thread block tile), from shared memory to the register file (thread block tile to warp tile), and from the register file to the CUDA cores for computation (warp tile to thread tile).
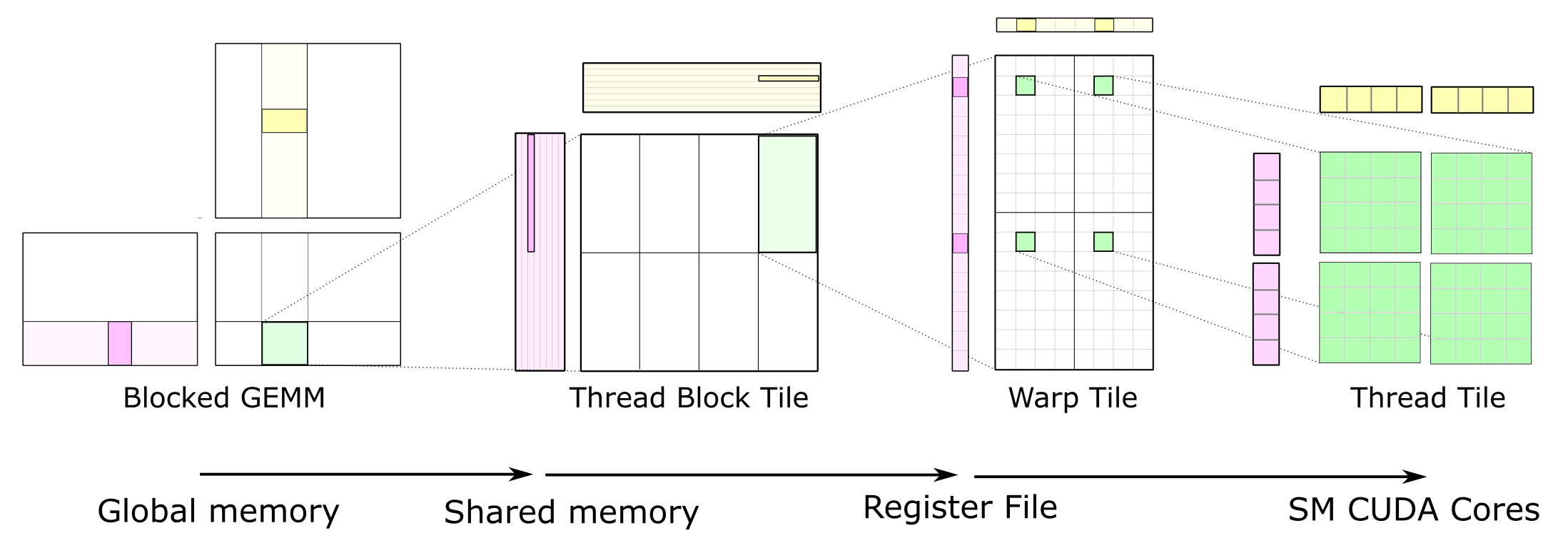
Thread Block Tile
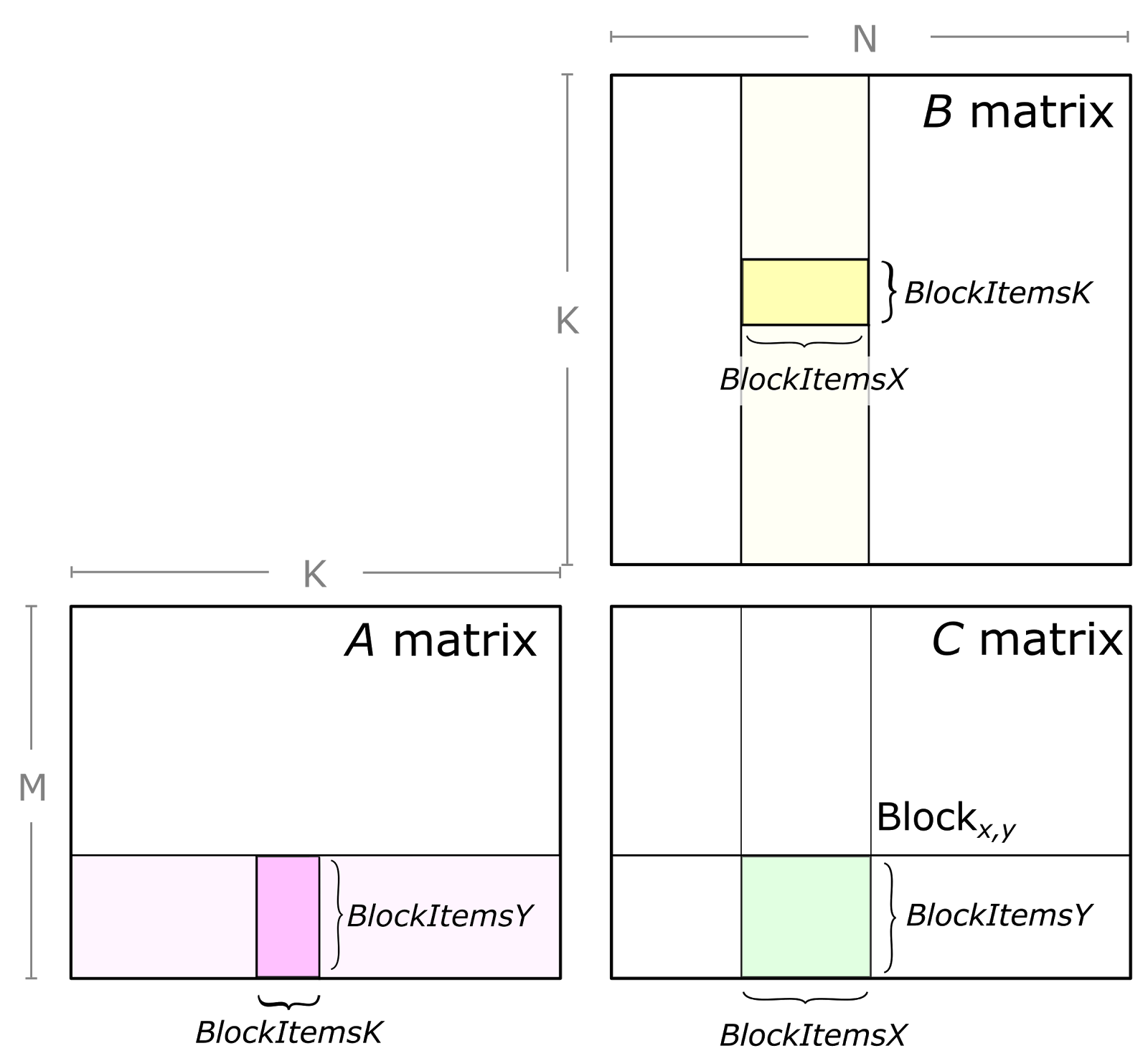
Each thread block computes its part of the output GEMM by iteratively loading blocks of matrix data from the input matrices and computing an accumulated matrix product (C += A * B). Figure 2 shows the computation performed by a single thread block and highlights the blocks of data used in one iteration of its main loop.
The CUDA thread block tile structure is further partitioned into warps (groups of threads that execute together in SIMT fashion). Warps provide a helpful organization for the GEMM computation and are an explicit part of the WMMA API, as we shall discuss shortly.
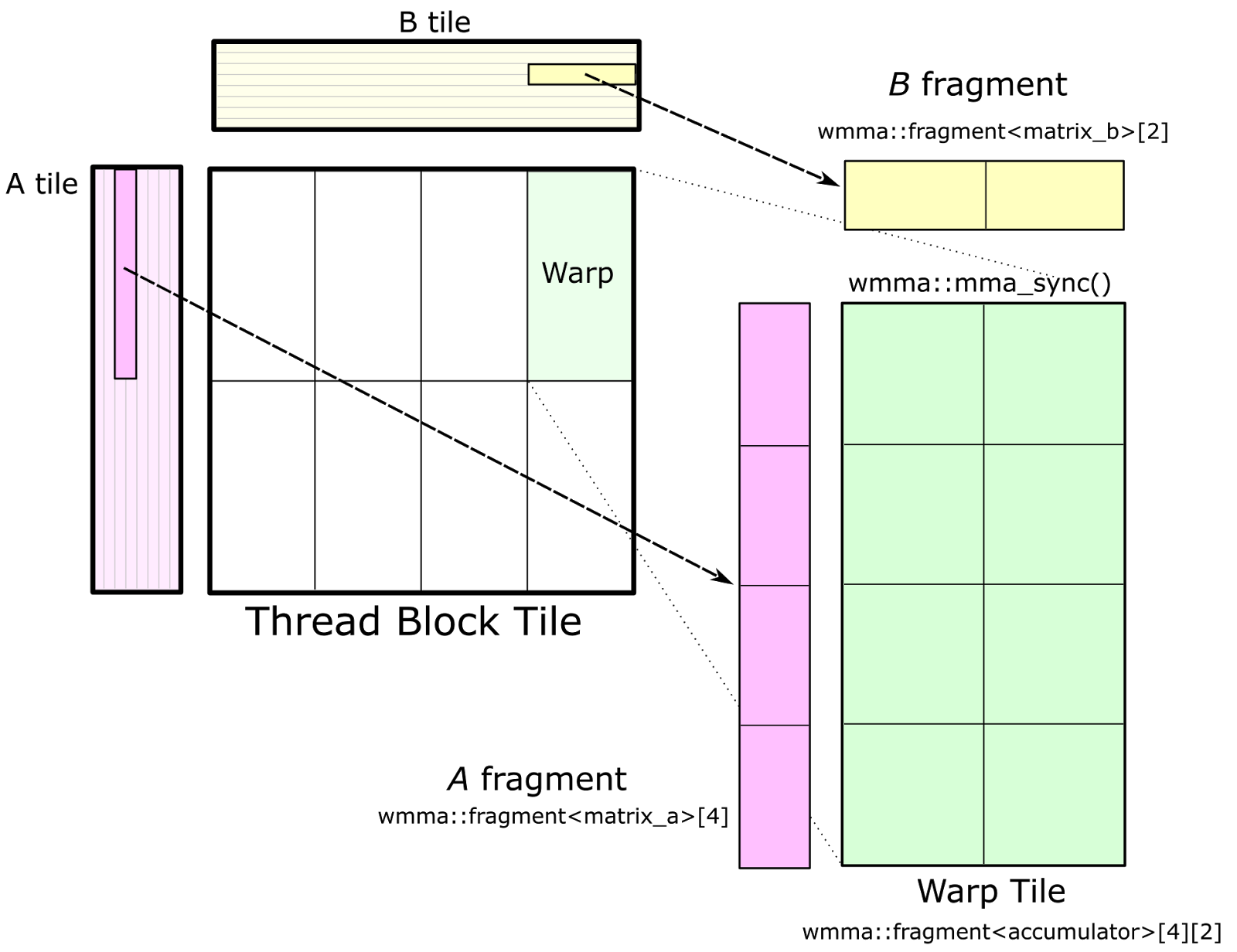
Figure 3 shows a detailed view of the structure of one block-level matrix product. Tiles of A and B are loaded from global memory and stored into shared memory accessible by all warps. The thread block’s output tile is spatially partitioned across warps as Figure 3 shows. We refer to storage for this output tile as accumulators because it stores the result of accumulated matrix products. Each accumulator is updated once per math operation, so it needs to reside in the fastest memory in the SM: the register file.
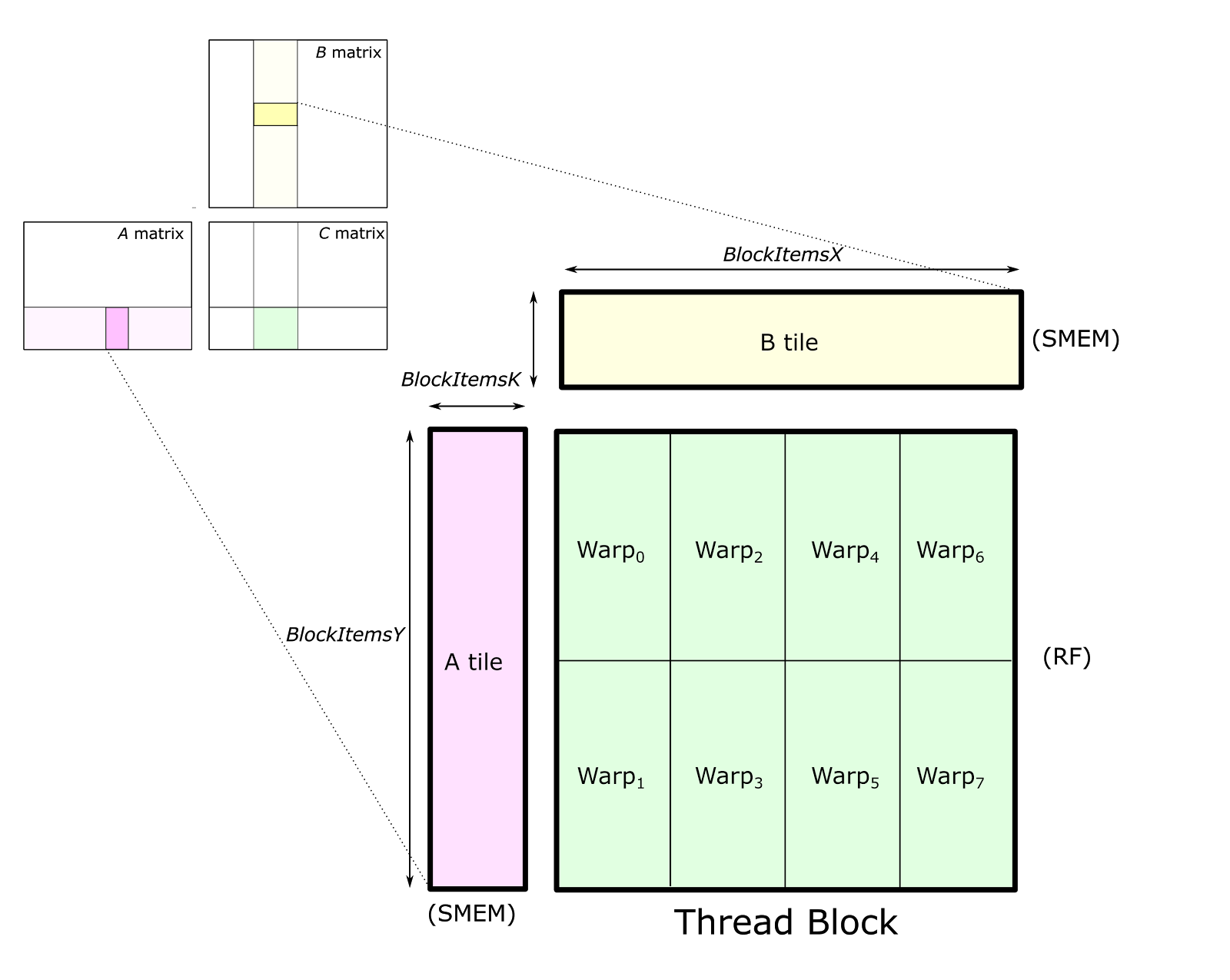
The parameters BlockItems{X,Y,K} are compile-time constants that the programmer specifies to tune the GEMM computation for the target processor and the aspect ratio of the specific GEMM configuration (e.g. M, N, K, data type, etc.). In the figure, we illustrate an eight-warp, 256-thread thread block which is typical for the large SGEMM (FP32 GEMM) tile size implemented in CUTLASS.
Warp Tile
Once data is stored in shared memory, each warp computes a sequence of accumulated matrix products by iterating over the K dimension of the thread block tile, loading submatrices (or fragments) from shared memory, and computing an accumulated outer product. Figure 4 shows a detailed view. The sizes of the fragments are typically very small in the K dimension to maximize the compute intensity relative to the amount of data loaded from shared memory, thereby avoiding shared memory bandwidth as a bottleneck.
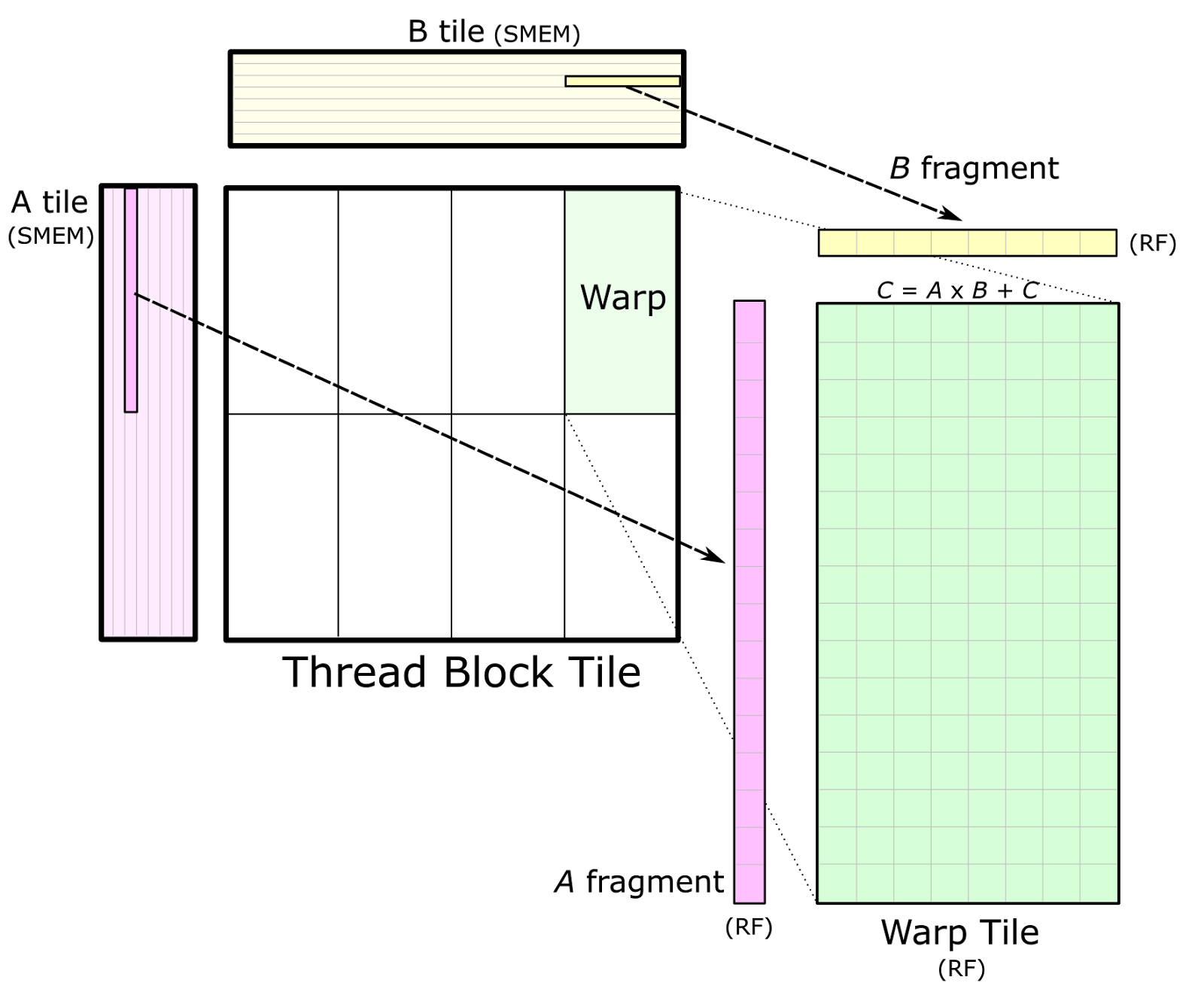
Figure 4 also depicts data sharing from shared memory among several warps. Warps in the same row of the thread block load the same fragments of A, and warps in the same column load the same fragments of B.
We note that the warp-centric organization of the GEMM structure is effective in implementing an efficient GEMM kernel but does not rely on implicit warp-synchronous execution for synchronization. CUTLASS GEMM kernels are well-synchronized with calls to __syncthreads() as appropriate.
Thread Tile
The CUDA Programming Model is defined in terms of thread blocks and individual threads. Consequently, the warp structure is mapped onto operations performed by individual threads. Threads cannot access each other’s registers, so we must choose an organization that enables values held in registers to be reused for multiple math instructions executed by the same thread. This leads to a 2D tiled structure within a thread as the detailed view in Figure 5 shows. Each thread issues a sequence of independent math instructions to the CUDA cores and computes an accumulated outer product.
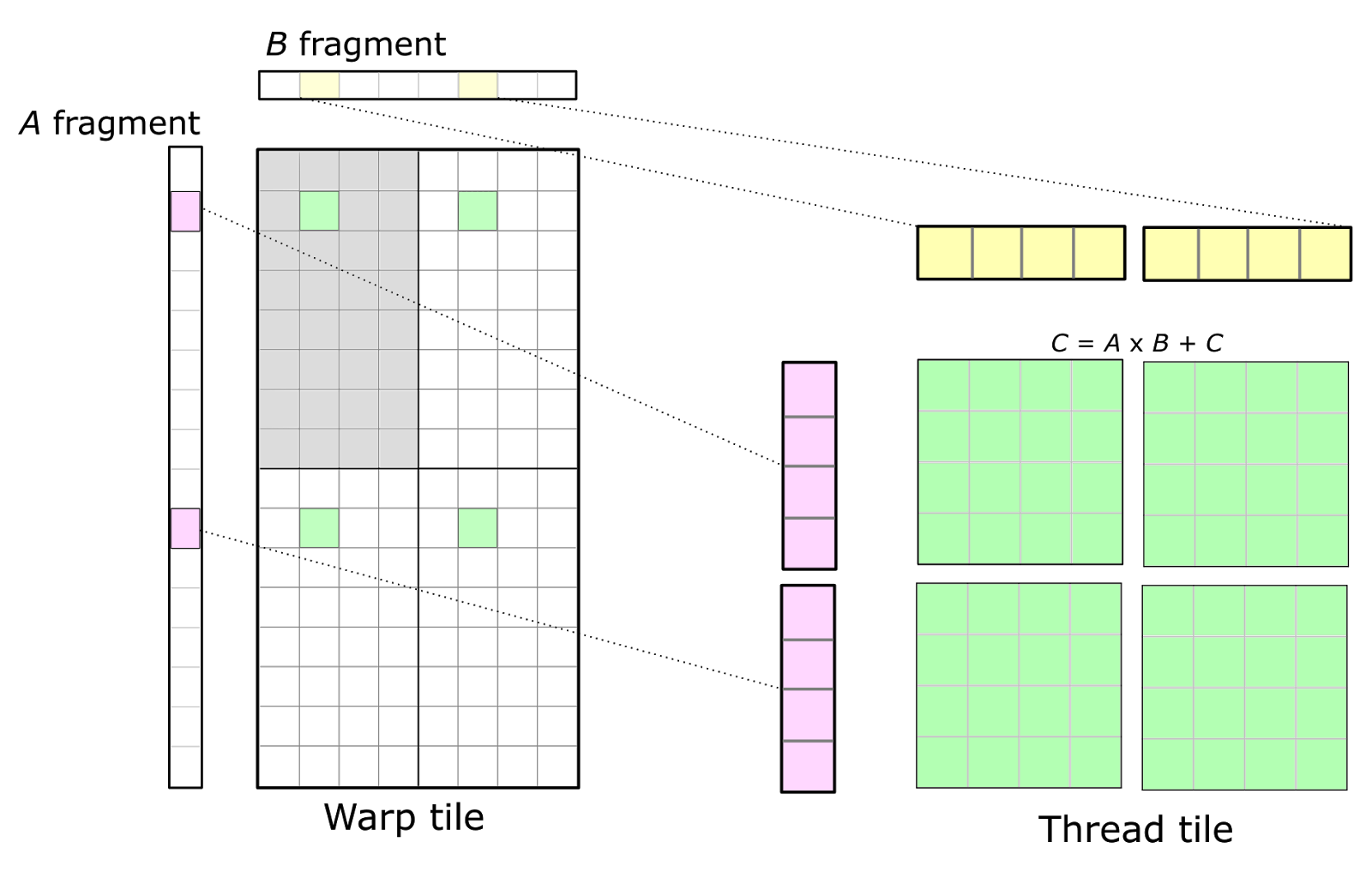
In Figure 5, the upper left quadrant of the warp is shaded in grey. The 32 cells correspond to the 32 threads within a warp. This arrangement leads to multiple threads within the same row or the same column fetching the same elements of the A and B fragments, respectively. To maximize compute intensity, this basic structure can be replicated to form the full warp-level accumulator tile, yielding an 8-by-8 overall thread tile computed from an outer product of 8-by-1 and 1-by-8 fragments. This is illustrated by the four accumulator tiles shown in green.
WMMA GEMM
The warp tile structure may be implemented with the CUDA Warp Matrix Multiply-Accumulate API (WMMA) introduced in CUDA 9 to target the Volta V100 GPU’s Tensor Cores. For more detail on the WMMA API, see the post Programming Tensor Cores in CUDA 9.
Each Tensor Core provides a 4x4x4 matrix processing array which performs the operation D = A * B + C, where A, B, C and D are 4×4 matrices as Figure 6 shows. The matrix multiply inputs A and B are FP16 matrices, while the accumulation matrices C and D may be FP16 or FP32 matrices.
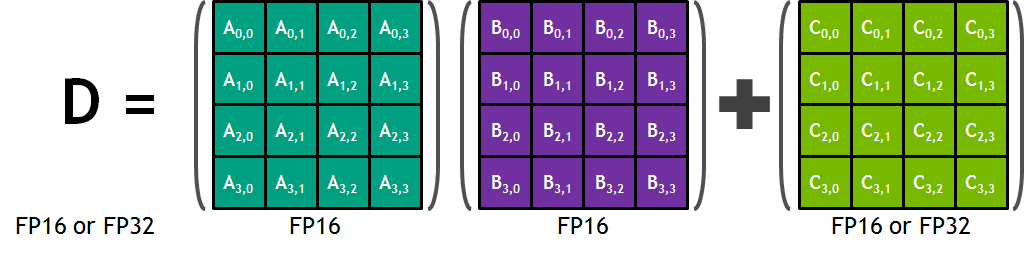
In effect, the WMMA API is an alternative to the thread tile structure described in the previous section for warp-wide matrix multiply-accumulate operations. Rather than decomposing the warp tile structure into scalar and vector elements owned by individual threads, the WMMA API provides an abstraction to the programmer for warp-cooperative matrix fragment load / store and multiply-accumulate math operations.
Figure 7 shows the warp tile structure that targets the CUDA WMMA API. Calls to wmma::load_matrix_sync load fragments of A and B into instances of the nvcuda::wmma::fragment<> template, and the accumulator elements for the warp tile are structured as an array of nvcuda::wmma::fragment<accumulator> objects. These fragments store a 2D matrix distributed among the threads of the warp. Finally, calls to nvcuda::wmma::mma_sync() for each accumulator fragment (and corresponding fragments from A and B) compute the warp-wide matrix multiply-accumulate operation using Tensor Cores.
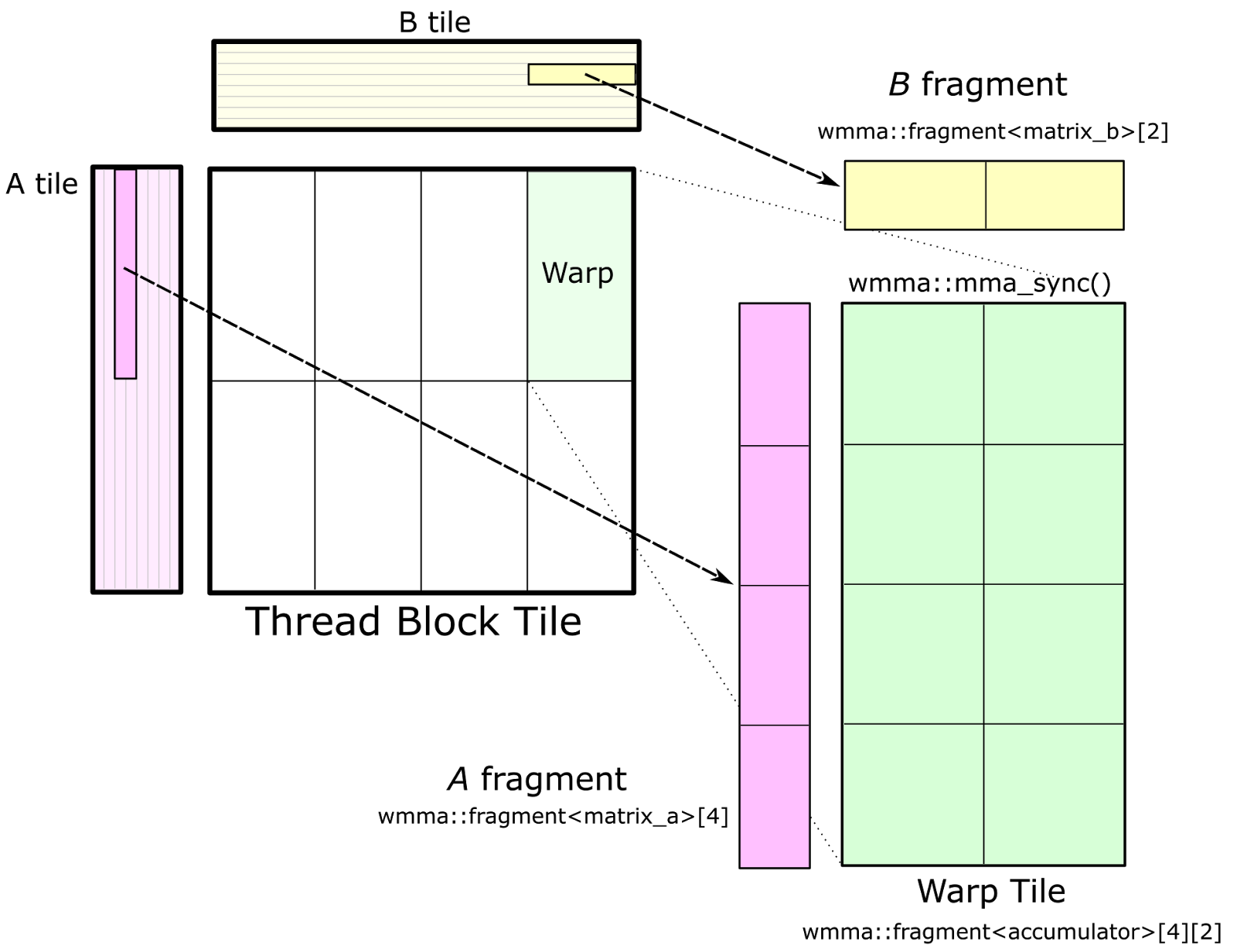
CUTLASS implements a GEMM based on the WMMA API in the file block_task_wmma.h. The warp tile must have dimensions that are multiples of matrix multiply-accumulate shapes defined by the nvcuda::wmma templates for the target CUDA Compute Capability. In CUDA 9.0, the fundamental WMMA size is 16-by-16-by-16.
Complete GEMM
The complete GEMM structure can be expressed as nested loops executed by the threads of a thread block, as the following listing shows. All loops except the outermost “main” loop have constant iteration counts and can be fully unrolled by the compiler. For brevity, address and index calculations are omitted here but are explained in the CUTLASS source code.
// Device function to compute a thread block’s accumulated matrix product
__device__ void block_matrix_product(int K_dim) {
// Fragments used to store data fetched from SMEM
value_t frag_a[ThreadItemsY];
value_t frag_b[ThreadItemsX];
// Accumulator storage
accum_t accumulator[ThreadItemsX][ThreadItemsY];
// GEMM Mainloop - iterates over the entire K dimension - not unrolled
for (int kblock = 0; kblock < K_dim; kblock += BlockItemsK) {
// Load A and B tiles from global memory and store to SMEM
//
// (not shown for brevity - see the CUTLASS source for more detail)
...
__syncthreads();
// Warp tile structure - iterates over the Thread Block tile
#pragma unroll
for (int warp_k = 0; warp_k < BlockItemsK; warp_k += WarpItemsK) {
// Fetch frag_a and frag_b from SMEM corresponding to k-index
//
// (not shown for brevity - see CUTLASS source for more detail)
...
// Thread tile structure - accumulate an outer product
#pragma unroll
for (int thread_x = 0; thread_x < ThreadItemsX; ++thread_x) {
#pragma unroll
for (int thread_y=0; thread_y < ThreadItemsY; ++thread_y) {
accumulator[thread_x][thread_y] += frag_a[y]*frag_b[x];
}
}
}
__syncthreads();
}
}
WarpItemsK refers to the target math operation’s dot product size. For SGEMM (FP32 GEMM), DGEMM (FP64), and HGEMM (FP16), the dot product length is 1 for scalar multiply-accumulate instructions. For IGEMM (8-bit integer GEMM), CUTLASS targets the four-element integer dot product instruction (IDP4A) with WarpItemsK=4. For WMMA-based GEMM, we choose the K dimension of the wmma::fragment<> template. Currently, this is defined as WarpItemsK=16.
Software Pipelining
Tiled matrix product makes extensive use of the register file to hold fragments and accumulator tiles as well as large shared memory allocations. Relatively high demand of on-chip storage limits occupancy, the maximum number of thread blocks that may run concurrently on one SM. Consequently, GEMM implementations can fit far fewer warps and thread blocks in each SM than is typical for GPU computing workloads. We use software pipelining to hide data movement latency by executing all stages of the GEMM hierarchy concurrently within a loop and feeding the output of each stage to its dependent stage during the next iteration as Figure 8 shows.
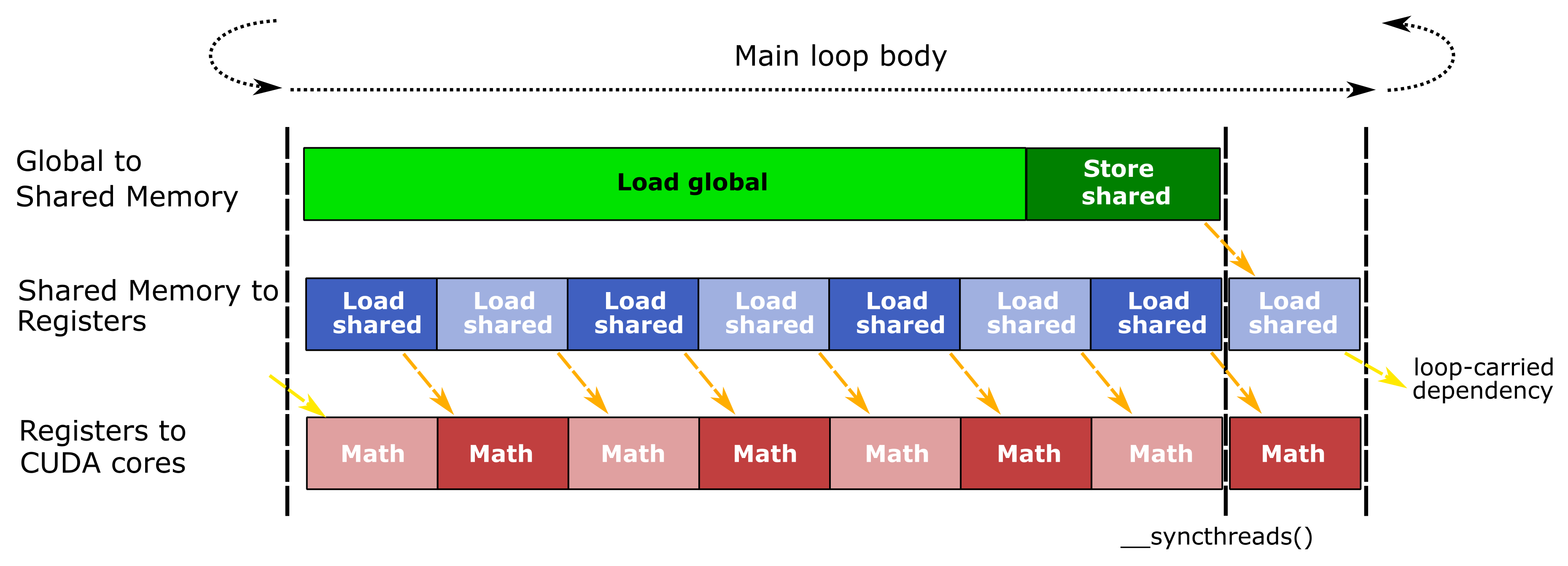
The GEMM CUDA kernel issues three concurrent streams of operations within the pipeline which correspond to the stages of dataflow within the GEMM hierarchy (Figure 1). The relative size of each stage in the illustration indicates whether the operation’s latency is long or short, and orange arrows highlight data dependencies between the stages of each stream. A call to__syncthreads() after data is stored to shared memory synchronizes all warps so they may read the shared memory without race conditions. The final math stage of the pipeline is overlapped with a load from shared memory which feeds data to the first math stage of the next main loop iteration.
Practically, CUDA programmers implement instruction-level concurrency among the pipe stages by interleaving CUDA statements for each stage in the program text and relying on the CUDA compiler to issue the proper instruction schedule in the compiled code. Extensive use of #pragma unroll and compile-time constants enables the CUDA compiler to unroll loops and map array elements to registers, both of which are critical to a tunable, efficient implementation. See block_task::consume_tile() for an example.
We use double buffering at each level of the GEMM hierarchy to enable the upstream pipeline stage to write data to shared memory or registers while the dependent pipeline stage loads from its storage elements. Notably, this eliminates the second __syncthreads() since one shared memory buffer is written while the other is read. The cost for double buffering is twice the shared memory capacity and twice the number of registers used to hold shared memory fetches.
The actual amount of latency hiding available depends on the sizes of the thread block, warp, and thread tiles as well as the throughput of the active math functional unit within the SM. While larger tiles yield more opportunity for data reuse and may offer more latency hiding, the physical capacities of the SM register file and shared memory limit the maximum tile size. Fortunately, NVIDIA GPUs have sufficient storage resources to execute GEMM tiles large enough to be math limited!
CUTLASS
CUTLASS is an implementation of the hierarchical GEMM structure as CUDA C++ template classes. We intend for these templates to be included in existing device-side CUDA kernels and functions, but we also provide a sample kernel and launch interface to get up and running quickly. Like CUB, extensive use of template arguments and compile-time constants enables CUTLASS to be tunable and flexible.
CUTLASS implements abstractions for the operations needed for efficient GEMM implementations. Specialized “tile loaders” move data efficiently from global memory into shared memory, accommodating the layouts of the source data while also enabling efficient, conflict-free loading into registers. For some layouts, IGEMM requires some restructuring of data to target CUDA’s 4-element integer dot product instruction, and this is done as the data is stored to SMEM.
CUTLASS GEMM Device Functions
The following example from dispatch.h defines a block_task type and instantiates a GEMM for floating-point data assuming column-major input matrices. The block_task_policy_t defines GEMM tile sizes and is discussed at length in the next section.
/// CUTLASS SGEMM example
__global__ void gemm_kernel(
float *C,
float const *A,
float const *B,
int M,
int N,
int K) {
// Define the GEMM tile sizes - discussed in next section
typedef block_task_policy <
128, // BlockItemsY: Height in rows of a tile
32, // BlockItemsX - Width in columns of a tile
8, // ThreadItemsY - Height in rows of a thread-tile
4, // ThreadItemsX - Width in columns of a thread-tile
8, // BlockItemsK - Depth of a tile
true, // UseDoubleScratchTiles - whether to double-buffer SMEM
block_raster_enum::Default // Block rasterization strategy
> block_task_policy_t;
// Define the epilogue functor
typedef gemm::blas_scaled_epilogue<float, float, float> epilogue_op_t ;
// Define the block_task type.
typedef block_task <
block_task_policy_t,
float,
float,
matrix_transform_t::NonTranspose,
4,
matrix_transform_t::NonTranspose,
4,
epilogue_op_t,
4,
true
> block_task_t;
// Declare statically-allocated shared storage
__shared__ block_task_t::scratch_storage_t smem;
// Construct and run the task
block_task_t(
reinterpret_cast(&smem),
&smem,
A,
B,
C,
epilogue_op_t(1, 0),
M,
N,
K).run();
}
The shared memory allocation smem is used by the block_task_t instance to store the thread block-level tiles in the matrix product computation.
epilogue_op_t is a template argument that specifies a functor which is used to update the output matrix after the matrix multiply operation is complete. This lets you easily compose matrix multiply with custom element-wise operations, as we describe in more detail later. CUTLASS provides the gemm::blas_scaled_epilogue functor implementation to compute the familiar GEMM operation C = alpha * AB + beta * C (defined in epilogue_function.h).
CUTLASS GEMM Policies
CUTLASS organizes compile-time constants specifying tile sizes at each level of the GEMM hierarchy as a specialization of the gemm::block_task_policy template which has the following declaration.
template <
int BlockItemsY, /// Height in rows of a tile in matrix C
int BlockItemsX, /// Width in columns of a tile in matrix C
int ThreadItemsY, /// Height in rows of a thread-tile in C
int ThreadItemsX, /// Width in columns of a thread-tile in C
int BlockItemsK, /// Number of K-split subgroups in a block
bool UseDoubleScratchTiles, /// Whether to double buffer shared memory
grid_raster_strategy::kind_t RasterStrategy /// Grid <a href="https://developer.nvidia.com/discover/ray-tracing">rasterization</a> strategy
> struct block_task_policy;
Policies for several valid GEMM blocking structures are defined in dispatch_policies.h, and we show one such policy below. This policy decomposes a matrix multiply operation into CUDA blocks, each spanning a 128-by-32 tile of the output matrix. The thread block tiles storing A and B have size 128-by-8 and 8-by-32, respectively. This policy is optimized for GEMM computations in which the C matrix is relatively narrow in its N dimension.
/// GEMM task policy specialization for tall SGEMM
template <>
struct gemm_policy<float, float, problem_size_t::Tall> :
block_task_policy<
128, // BlockItemsY - Height in rows of a tile
32, // BlockItemsX - Width in columns of a tile
8, // ThreadItemsY - Height in rows of a thread-tile
4, // ThreadItemsX - Width in columns of a thread-tile
8, // BlockItemsK - Depth of a tile
true, // UseDoubleScratchTiles - whether to double-buffer SMEM
grid_raster_strategy::Default> // Grid rasterization strategy
{};
The sizes of the thread tile fragments are ThreadItemsY-by-1 and ThreadItemsX-by-1, respectively. In the case of the example above, these are given as 8-by-1 vectors from A and 4-by-1 vectors from B.
With the policy type defined, we can define the type for gemm::block_task, a CUTLASS GEMM. This template has the following argument list.
template <
/// Parameterization of block_task_policy
typename block_task_policy_t,
/// Multiplicand value type (matrices A and B)
typename value_t,
/// Accumulator value type (matrix C and scalars)
typename accum_t,
/// Layout enumerant for matrix A
matrix_transform_t::kind_t TransformA,
/// Alignment (in bytes) for A operand
int LdgAlignA,
/// Layout enumerant for matrix B
matrix_transform_t::kind_t TransformB,
/// Alignment (in bytes) for B operand
int LdgAlignB,
/// Epilogue functor applied to matrix product
typename epilogue_op_t,
/// Alignment (in bytes) for C operand
int LdgAlignC,
/// Whether GEMM supports matrix sizes other than mult of BlockItems{XY}
bool Ragged
> struct block_task;
value_t and accum_t specify the types of source operands and accumulator matrices, respectively. TransformA and TransformB specify the layout of operands A and B, respectively. Though we have not discussed matrix layout in detail, CUTLASS supports all combinations of row-major and column-major input matrices.
LdgAlignA and LdgAlignB specify guaranteed alignment, which enables the CUTLASS device code to use vector memory operations. An alignment of 8 bytes, for example, permits CUTLASS to load elements of type float in two-element vectors. This reduces code size and improves performance by reducing the number of memory operations in flight within the GPU. More critically, ragged handling indicates whether matrix dimensions may be arbitrary sizes (satisfying alignment guarantees). If this template argument is false`, matrices A, B, and C are all expected to have dimensions that are multiples of the tile parameters in the block_task_policy.
Fusing Element-wise Operations with SGEMM
Deep Learning computations typically perform simple element-wise operations after GEMM computations, such as computing an activation function. These bandwidth-limited layers can be fused into the end of the GEMM operation to eliminate an extra kernel launch and avoid a round trip through global memory.
The following example demonstrates a simple application of the GEMM template that adds a bias term to the scaled matrix product and then applies the ReLU function to clamp the result to non-negative values. By separating the epilogue into a functor, passing arguments such as pointers to additional matrix and tensor arguments or additional scale factors is straightforward and does not encumber the GEMM implementation.
First, we define a class that implements the gemm::epilogue_op concept. The constructor and other methods aren’t shown here, but the element-wise bias and ReLU operations are shown in the implementation of the function call operator.
template <typename accum_t, typename scalar_t, typename output_t>
struct fused_bias_relu_epilogue {
// Data members pass additional arguments to epilogue
scalar_t const *Bias;
accum_t threshold;
/// Constructor callable on host and device initializes data members
inline __device__ __host__
fused_bias_relu_epilogue(
scalar_t const *Bias,
accum_t threshold
): Bias(Bias), threshold(threshold) { }
/// Applies bias + ReLu operation
inline __device__ __host__
output_t operator()(
accum_t accumulator, /// element of matrix product result
output_t c, /// element of source accumulator matrix C
size_t idx /// index of c element; may be used to load
/// elements from other identically-
/// structured matrices
) const {
// Compute the result by scaling the matrix product, adding bias,
// and adding the scaled accumulator element.
accum_t result = output_t(
alpha * scalar_t(accumulator) +
Bias[i] + // load and add the bias
beta * scalar_t(c)
);
// apply clamping function
return max(threshold, result);
}
};
Then we apply that operator as the epilogue operation.
// New: define type for custom epilogue functor
typedef fused_bias_relu_epilogue_t<float, float, float>
bias_relu_epilogue_t;
/// Computes GEMM fused with Bias and ReLu operation
__global__ void gemm_bias_relu(
..., /// GEMM parameters not shown
bias_relu_epilogue_t bias_relu_op) { /// bias_relu_op constructed
/// by caller
// Define the block_task type.
typedef block_task<
block_task_policy_t, // same policy as previous example
float,
float,
matrix_transform_t::NonTranspose,
4,
matrix_transform_t::NonTranspose,
4,
bias_relu_epilogue_t, // New: custom epilogue functor type
4,
true
> block_task_t ;
// Declare statically-allocated shared storage
__shared__ block_task_t::scratch_storage_t smem;
// Construct and run the task
block_task_t(
reinterpret_cast(&smem),
&smem,
A,
B,
C,
bias_relu_op, // New: custom epilogue object
M,
N,
K).run();
}
This simple example demonstrates the value of combining generic programming techniques with efficient GEMM implementations.
Tesla V100 (Volta) Performance
CUTLASS is very efficient, with performance comparable to cuBLAS for scalar GEMM computations. Figure 9 shows CUTLASS performance relative to cuBLAS compiled with CUDA 9.0 running on an NVIDIA Tesla V100 GPU for large matrix dimensions (M=10240, N=K=4096). Figure 9 shows relative performance for each compute data type CUTLASS supports and all permutations of row-major and column-major layouts for input operands.
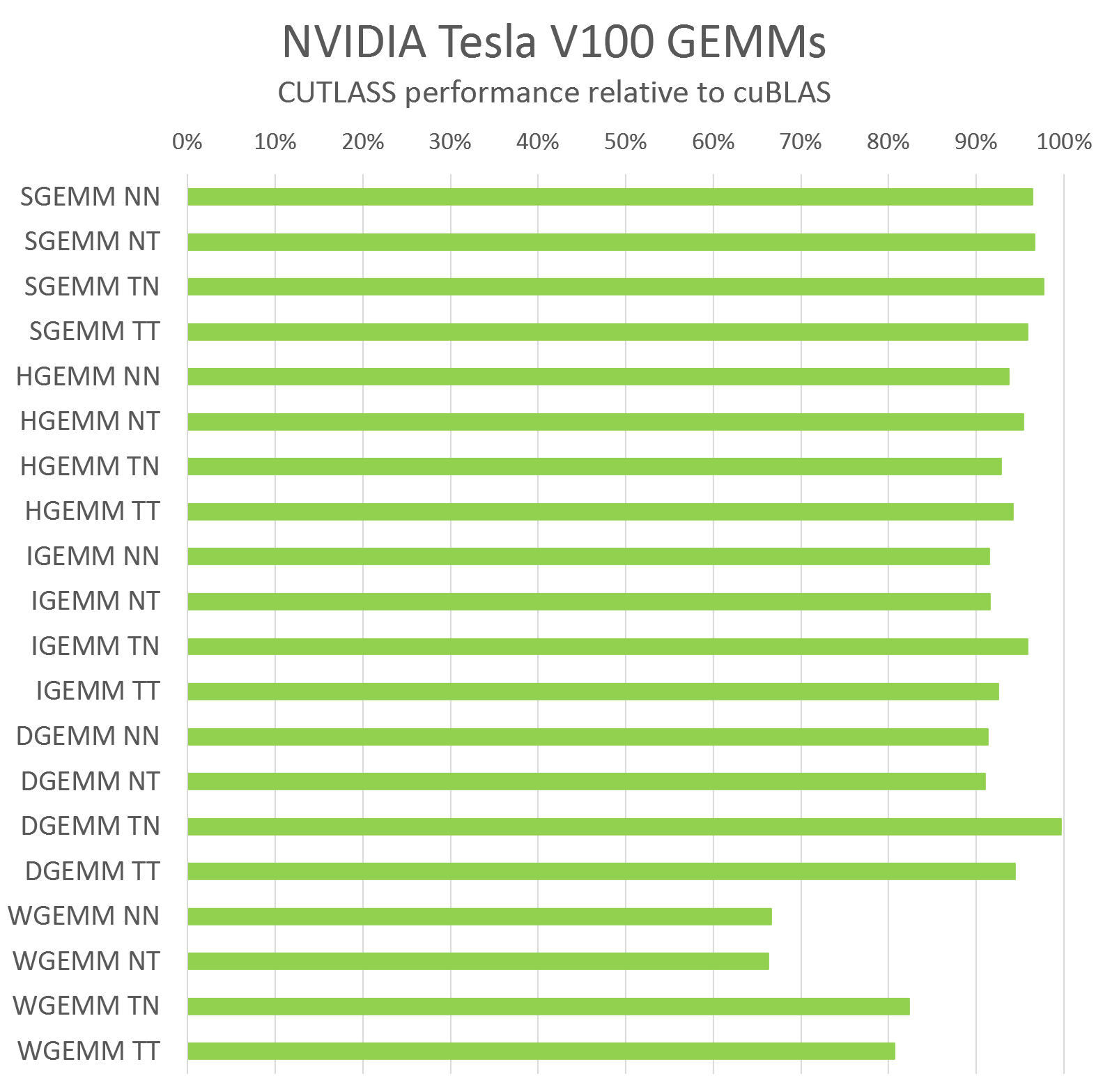
In most cases, CUTLASS C++ achieves within a few percent of the performance of the hand-tuned assembly kernels in cuBLAS. For WMMA GEMM (WGEMM in Figure 9), CUTLASS does not yet achieve the same performance as cuBLAS, but we are working closely with the CUDA compiler and GPU architecture teams to develop techniques to reach a similar level of performance in CUDA code.
Try CUTLASS Today!
There are many interesting details we haven’t addressed in this blog post, so we recommend you check out the CUTLASS repository and try out CUTLASS yourself. The cutlass_test sample program demonstrates calling CUTLASS GEMM kernels, verifying their result, and measuring their performance. Look forward to future updates from us, and feel free to send us feedback or reach out using the comments below!
Acknowledgements
Special thanks to Joel McCormack for his technical insight and explication, particularly with respect to NVIDIA microarchitecture and the techniques employed by cuBLAS and cuDNN.
References
[1] Sharan Chetlur, Cliff Woolley, Philippe Vandermersch, Jonathan Cohen, John Tran, Bryan Catanzaro, Evan Shelhamer. cuDNN: Efficient Primitives for Deep Learning, arXiv:1410.0759, 2014.
[2] Michael Mathieu, Mikael Henaff, Yann LeCun. Fast training of Convolutional Networks through FFTs. arXiv:1312.5851. 2013.
[3] Andrew Lavin, Scott Gray. Fast Algorithms for Convolutional Neural Networks. arXiv:1509.09308. 2015.
[4] MAGMA. http://icl.cs.utk.edu/magma/index.html