This post is a super simple introduction to CUDA, the popular parallel computing platform and programming model from NVIDIA. I wrote a previous post, Easy Introduction to CUDA in 2013 that has been popular over the years. But CUDA programming has gotten easier, and GPUs have gotten much faster, so it’s time for an updated (and even easier) introduction.
CUDA C++ is just one of the ways you can create massively parallel applications with CUDA. It lets you use the powerful C++ programming language to develop high performance algorithms accelerated by thousands of parallel threads running on GPUs. Many developers have accelerated their computation- and bandwidth-hungry applications this way, including the libraries and frameworks that underpin the ongoing revolution in artificial intelligence known as Deep Learning.
So, you’ve heard about CUDA and you are interested in learning how to use it in your own applications. If you are a C or C++ programmer, this blog post should give you a good start. To follow along, you’ll need a computer with an CUDA-capable GPU (Windows, Mac, or Linux, and any NVIDIA GPU should do), or a cloud instance with GPUs (AWS, Azure, IBM SoftLayer, and other cloud service providers have them). You’ll also need the free CUDA Toolkit installed. You can also follow along with a Jupyter Notebook running on a GPU in the cloud.
Let’s get started!

Starting Simple
We’ll start with a simple C++ program that adds the elements of two arrays with a million elements each.
#include <iostream>
#include <math.h>
// function to add the elements of two arrays
void add(int n, float *x, float *y)
{
for (int i = 0; i < n; i++)
y[i] = x[i] + y[i];
}
int main(void)
{
int N = 1<<20; // 1M elements
float *x = new float[N];
float *y = new float[N];
// initialize x and y arrays on the host
for (int i = 0; i < N; i++) {
x[i] = 1.0f;
y[i] = 2.0f;
}
// Run kernel on 1M elements on the CPU
add(N, x, y);
// Check for errors (all values should be 3.0f)
float maxError = 0.0f;
for (int i = 0; i < N; i++)
maxError = fmax(maxError, fabs(y[i]-3.0f));
std::cout << "Max error: " << maxError << std::endl;
// Free memory
delete [] x;
delete [] y;
return 0;
}
First, compile and run this C++ program. Put the code above in a file and save it as add.cpp, and then compile it with your C++ compiler. I’m on a Mac so I’m using clang++, but you can use g++ on Linux or MSVC on Windows.
> clang++ add.cpp -o add
Then run it:
> ./add Max error: 0.000000
(On Windows you may want to name the executable add.exe and run it with .\add.)
As expected, it prints that there was no error in the summation and then exits. Now I want to get this computation running (in parallel) on the many cores of a GPU. It’s actually pretty easy to take the first steps.
First, I just have to turn our add function into a function that the GPU can run, called a kernel in CUDA. To do this, all I have to do is add the specifier __global__ to the function, which tells the CUDA C++ compiler that this is a function that runs on the GPU and can be called from CPU code.
// CUDA Kernel function to add the elements of two arrays on the GPU
__global__
void add(int n, float *x, float *y)
{
for (int i = 0; i < n; i++)
y[i] = x[i] + y[i];
}
These __global__ functions are known as kernels, and code that runs on the GPU is often called device code, while code that runs on the CPU is host code.
Memory Allocation in CUDA
To compute on the GPU, I need to allocate memory accessible by the GPU. Unified Memory in CUDA makes this easy by providing a single memory space accessible by all GPUs and CPUs in your system. To allocate data in unified memory, call cudaMallocManaged(), which returns a pointer that you can access from host (CPU) code or device (GPU) code. To free the data, just pass the pointer to cudaFree().
I just need to replace the calls to new in the code above with calls to cudaMallocManaged(), and replace calls to delete [] with calls to cudaFree.
// Allocate Unified Memory -- accessible from CPU or GPU float *x, *y; cudaMallocManaged(&x, N*sizeof(float)); cudaMallocManaged(&y, N*sizeof(float)); ... // Free memory cudaFree(x); cudaFree(y);
Finally, I need to launch the add() kernel, which invokes it on the GPU. CUDA kernel launches are specified using the triple angle bracket syntax <<< >>>. I just have to add it to the call to add before the parameter list.
add<<<1, 1>>>(N, x, y);
Easy! I’ll get into the details of what goes inside the angle brackets soon; for now all you need to know is that this line launches one GPU thread to run add().
Just one more thing: I need the CPU to wait until the kernel is done before it accesses the results (because CUDA kernel launches don’t block the calling CPU thread). To do this I just call cudaDeviceSynchronize() before doing the final error checking on the CPU.
Here’s the complete code:
#include <iostream>
#include <math.h>
// Kernel function to add the elements of two arrays
__global__
void add(int n, float *x, float *y)
{
for (int i = 0; i < n; i++)
y[i] = x[i] + y[i];
}
int main(void)
{
int N = 1<<20;
float *x, *y;
// Allocate Unified Memory – accessible from CPU or GPU
cudaMallocManaged(&x, N*sizeof(float));
cudaMallocManaged(&y, N*sizeof(float));
// initialize x and y arrays on the host
for (int i = 0; i < N; i++) {
x[i] = 1.0f;
y[i] = 2.0f;
}
// Run kernel on 1M elements on the GPU
add<<<1, 1>>>(N, x, y);
// Wait for GPU to finish before accessing on host
cudaDeviceSynchronize();
// Check for errors (all values should be 3.0f)
float maxError = 0.0f;
for (int i = 0; i < N; i++)
maxError = fmax(maxError, fabs(y[i]-3.0f));
std::cout << "Max error: " << maxError << std::endl;
// Free memory
cudaFree(x);
cudaFree(y);
return 0;
}
CUDA files have the file extension .cu. So save this code in a file called add.cu and compile it with nvcc, the CUDA C++ compiler.
> nvcc add.cu -o add_cuda > ./add_cuda Max error: 0.000000
This is only a first step, because as written, this kernel is only correct for a single thread, since every thread that runs it will perform the add on the whole array. Moreover, there is a race condition since multiple parallel threads would both read and write the same locations.
Note: on Windows, you need to make sure you set Platform to x64 in the Configuration Properties for your project in Microsoft Visual Studio.
Profile it!
I think the simplest way to find out how long the kernel takes to run is to run it with nvprof, the command line GPU profiler that comes with the CUDA Toolkit. Just type nvprof ./add_cuda on the command line:
$ nvprof ./add_cuda ==3355== NVPROF is profiling process 3355, command: ./add_cuda Max error: 0 ==3355== Profiling application: ./add_cuda ==3355== Profiling result: Time(%) Time Calls Avg Min Max Name 100.00% 463.25ms 1 463.25ms 463.25ms 463.25ms add(int, float*, float*) ...
Above is the truncated output from nvprof, showing a single call to add. It takes about half a second on an NVIDIA Tesla K80 accelerator, and about the same time on an NVIDIA GeForce GT 740M in my 3-year-old Macbook Pro.
Let’s make it faster with parallelism.
Picking up the Threads
Now that you’ve run a kernel with one thread that does some computation, how do you make it parallel? The key is in CUDA’s <<<1, 1>>>syntax. This is called the execution configuration, and it tells the CUDA runtime how many parallel threads to use for the launch on the GPU. There are two parameters here, but let’s start by changing the second one: the number of threads in a thread block. CUDA GPUs run kernels using blocks of threads that are a multiple of 32 in size, so 256 threads is a reasonable size to choose.
add<<<1, 256>>>(N, x, y);
If I run the code with only this change, it will do the computation once per thread, rather than spreading the computation across the parallel threads. To do it properly, I need to modify the kernel. CUDA C++ provides keywords that let kernels get the indices of the running threads. Specifically, threadIdx.x contains the index of the current thread within its block, and blockDim.x contains the number of threads in the block. I’ll just modify the loop to stride through the array with parallel threads.
__global__
void add(int n, float *x, float *y)
{
int index = threadIdx.x;
int stride = blockDim.x;
for (int i = index; i < n; i += stride)
y[i] = x[i] + y[i];
}
The add function hasn’t changed that much. In fact, setting index to 0 and stride to 1 makes it semantically identical to the first version.
Save the file as add_block.cu and compile and run it in nvprof again. For the remainder of the post I’ll just show the relevant line from the output.
Time(%) Time Calls Avg Min Max Name 100.00% 2.7107ms 1 2.7107ms 2.7107ms 2.7107ms add(int, float*, float*)
That’s a big speedup (463ms down to 2.7ms), but not surprising since I went from 1 thread to 256 threads. The K80 is faster than my little Macbook Pro GPU (at 3.2ms). Let’s keep going to get even more performance.
Out of the Blocks
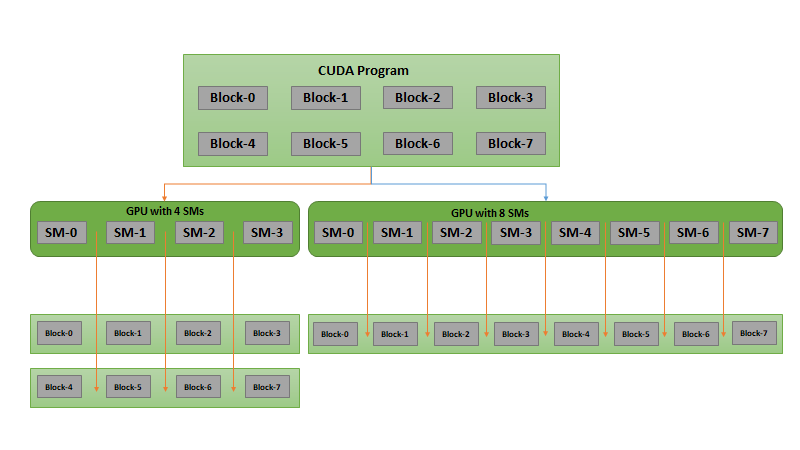
CUDA GPUs have many parallel processors grouped into Streaming Multiprocessors, or SMs. Each SM can run multiple concurrent thread blocks. As an example, a Tesla P100 GPU based on the Pascal GPU Architecture has 56 SMs, each capable of supporting up to 2048 active threads. To take full advantage of all these threads, I should launch the kernel with multiple thread blocks.
By now you may have guessed that the first parameter of the execution configuration specifies the number of thread blocks. Together, the blocks of parallel threads make up what is known as the grid. Since I have N elements to process, and 256 threads per block, I just need to calculate the number of blocks to get at least N threads. I simply divide N by the block size (being careful to round up in case N is not a multiple of blockSize).
int blockSize = 256; int numBlocks = (N + blockSize - 1) / blockSize; add<<<numBlocks, blockSize>>>(N, x, y);

I also need to update the kernel code to take into account the entire grid of thread blocks. CUDA provides gridDim.x, which contains the number of blocks in the grid, and blockIdx.x, which contains the index of the current thread block in the grid. Figure 1 illustrates the the approach to indexing into an array (one-dimensional) in CUDA using blockDim.x, gridDim.x, and threadIdx.x. The idea is that each thread gets its index by computing the offset to the beginning of its block (the block index times the block size: blockIdx.x * blockDim.x) and adding the thread’s index within the block (threadIdx.x). The code blockIdx.x * blockDim.x + threadIdx.x is idiomatic CUDA.
__global__
void add(int n, float *x, float *y)
{
int index = blockIdx.x * blockDim.x + threadIdx.x;
int stride = blockDim.x * gridDim.x;
for (int i = index; i < n; i += stride)
y[i] = x[i] + y[i];
}
The updated kernel also sets stride to the total number of threads in the grid (blockDim.x * gridDim.x). This type of loop in a CUDA kernel is often called a grid-stride loop.
Save the file as add_grid.cu and compile and run it in nvprof again.
Time(%) Time Calls Avg Min Max Name 100.00% 94.015us 1 94.015us 94.015us 94.015us add(int, float*, float*)
That’s another 28x speedup, from running multiple blocks on all the SMs of a K80! We’re only using one of the 2 GPUs on the K80, but each GPU has 13 SMs. Note the GeForce in my laptop has 2 (weaker) SMs and it takes 680us to run the kernel.
Summing Up
Here’s a rundown of the performance of the three versions of the add() kernel on the Tesla K80 and the GeForce GT 750M.
| Laptop (GeForce GT 750M) | Server (Tesla K80) | |||
|---|---|---|---|---|
| Version | Time | Bandwidth | Time | Bandwidth |
| 1 CUDA Thread | 411ms | 30.6 MB/s | 463ms | 27.2 MB/s |
| 1 CUDA Block | 3.2ms | 3.9 GB/s | 2.7ms | 4.7 GB/s |
| Many CUDA Blocks | 0.68ms | 18.5 GB/s | 0.094ms | 134 GB/s |
As you can see, we can achieve very high bandwidth on GPUs. The computation in this post is very bandwidth-bound, but GPUs also excel at heavily compute-bound computations such as dense matrix linear algebra, deep learning, image and signal processing, physical simulations, and more.
Exercises
To keep you going, here are a few things to try on your own. Please post about your experience in the comments section below.
- Browse the CUDA Toolkit documentation. If you haven’t installed CUDA yet, check out the Quick Start Guide and the installation guides. Then browse the Programming Guide and the Best Practices Guide. There are also tuning guides for various architectures.
- Experiment with
printf()inside the kernel. Try printing out the values ofthreadIdx.xandblockIdx.xfor some or all of the threads. Do they print in sequential order? Why or why not? - Print the value of
threadIdx.yorthreadIdx.z(orblockIdx.y) in the kernel. (Likewise forblockDimandgridDim). Why do these exist? How do you get them to take on values other than 0 (1 for the dims)? - If you have access to a Pascal-based GPU, try running
add_grid.cuon it. Is performance better or worse than the K80 results? Why? (Hint: read about Pascal’s Page Migration Engine and the CUDA 8 Unified Memory API.) For a detailed answer to this question, see the post Unified Memory for CUDA Beginners.
Where To From Here?
I hope that this post has whet your appetite for CUDA and that you are interested in learning more and applying CUDA C++ in your own computations. If you have questions or comments, don’t hesitate to reach out using the comments section below.
I plan to follow up this post with further CUDA programming material, but to keep you busy for now, there is a whole series of older introductory posts that you can continue with (and that I plan on updating / replacing in the future as needed):
- How to Implement Performance Metrics in CUDA C++
- How to Query Device Properties and Handle Errors in CUDA C++
- How to Optimize Data Transfers in CUDA C++
- How to Overlap Data Transfers in CUDA C++
- How to Access Global Memory Efficiently in CUDA C++
- Using Shared Memory in CUDA C++
- An Efficient Matrix Transpose in CUDA C++
- Finite Difference Methods in CUDA C++, Part 1
- Finite Difference Methods in CUDA C++, Part 2
- Accelerated Ray Tracing in One Weekend with CUDA
There is also a series of CUDA Fortran posts mirroring the above, starting with An Easy Introduction to CUDA Fortran.
You might also be interested in signing up for the online course on CUDA programming from Udacity and NVIDIA.
There is a wealth of other content on CUDA C++ and other GPU computing topics here on the NVIDIA Developer Blog, so look around!
If you enjoyed this notebook and want to learn more, the NVIDIA DLI offers several in-depth CUDA programming courses.
- For those of you just starting out, see Fundamentals of Accelerated Computing with CUDA C/C++, which provides dedicated GPU resources, a more sophisticated programming environment, use of the NVIDIA Nsight Systems visual profiler, dozens of interactive exercises, detailed presentations, over 8 hours of material, and the ability to earn a DLI Certificate of Competency.
- For Python programmers, see Fundamentals of Accelerated Computing with CUDA Python.
- For more intermediate and advanced CUDA programming materials, see the Accelerated Computing section of the NVIDIA DLI self-paced catalog.