Sometimes you need to use small per-thread arrays in your GPU kernels. The performance of accessing elements in these arrays can vary depending on a number of factors. In this post I’ll cover several common scenarios ranging from fast static indexing to more complex and challenging use cases.
Static indexing
Before discussing dynamic indexing let’s briefly look at static indexing. For small arrays where all indices are known constants at compile time, as in the following sample code, the compiler places all accessed elements of the array into registers.
__global__ void kernel1(float * buf)
{
float a[2];
...
float sum = a[0] + a[1];
...
}
This way array elements are accessed in the fastest way possible: math instructions use the data directly without loads and stores.
A slightly more complex (and probably more useful) case is an unrolled loop over the indices of the array. In the following code the compiler is also capable of assigning the accessed array elements to registers.
__global__ void kernel2(float * buf)
{
float a[5];
...
float sum = 0.0f;
#pragma unroll
for(int i = 0; i < 5; ++i)
sum += a[i];
...
}
Here we tell the compiler to unroll the loop with the directive #pragma unroll, effectively replacing the loop with all the iterations listed explicitly, as in the following snippet.
sum += a[0]; sum += a[1]; sum += a[2]; sum += a[3]; sum += a[4];
All the indices are now constants, so the compiler puts the whole array into registers. I ran a Kernel Profile experiment in the NVIDIA Visual Profiler. When you enable source line information in the binary by building the CUDA source files with the -lineinfo nvcc option lets the Visual Profiler show the correspondence between the CUDA C++ source code lines and the generated assembler instructions. For the unrolled loop above, the compiler is able to generate just 4 floating point add instructions, without any stores and loads. Why 4 instructions when we have 5 additions? The compiler is smart enough to figure out that adding 0.0f to a[0] is just a[0] and it eliminates this instruction. See the screenshot of Kernel Profile experiment in Figure 1.
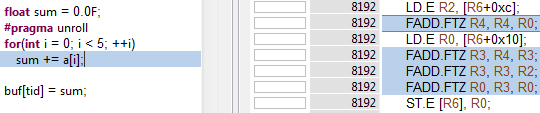
In some cases the compiler can unroll the loop automatically without #pragma unroll. Note that the array size must be an immediate numeric constant; however you can define it via a #define or a template parameter to the kernel.
Dynamic indexing with Uniform Access
When the compiler can’t resolve array indices to constants it must put private arrays into GPU local memory. “Local” here doesn’t mean this memory is close to compute units, necessarily; it means that it is local to each thread and not visible to other threads. Logical local memory actually resides in global GPU memory. Each thread has its own copy of any local array, and the compiler generates load and store instructions for array reads and writes, respectively.
Using local memory is slower than keeping array elements directly in registers, but if you have sufficient math instructions in your kernel and enough threads to hide the latency, the local load/store instructions may be a minor cost. Empiricially, a 4:1 to 8:1 ratio of math to memory operations should be enough, the exact number depends on your particular kernel and GPU architecture. Your kernel should also have occupancy high enough to hide local memory access latencies.
Here is an example of a kernel where the compiler can’t resolve indices to constants even if it unrolls the loop.
__global__ void kernel3(float * buf, int start_index)
{
float a[6];
...
float sum = 0.0f;
#pragma unroll
for(int i = 0; i < 5; ++i)
sum += a[start_index + i];
...
}
A Kernel Profile experiment confirms that each access to array a now results in a local load or store, as Figure 2 shows.
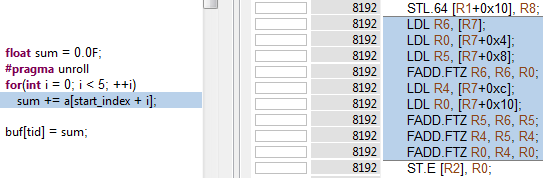
Note that this example demonstrates uniform access: all threads of each warp access elements of their own private array using the same index (even if this index is calculated dynamically at runtime). This enables the GPU load/store units to execute the instructions in the most efficient way.
Local memory is cached in the GPU’s L2 & L1 caches. As the size of your private array grows it will exceed the size of the L1 cache and then the L2 cache until eventually accesses will pay the full price of accessing global memory. To partly mitigate this problem you can use cudaFuncSetCacheConfig with cudaFuncCachePreferL1 to tell the CUDA runtime to configure a larger L1 cache and smaller shared memory. Please note that shared memory and L1 cache are physically separate in the Maxwell architecture, so this function has no effect for these chips.
Dynamic Indexing with Non-Uniform Access
Things get more difficult when threads of a warp start accessing elements of their private arrays using different indices. This is called non-uniform indexing. When this happens, the SM must “replay” load/store instructions for each unique index used by the threads in the warp. This is more common with data-dependent algorithms like the following example, where each thread reads its index from the global memory array indexbuf.
#define ARRAY_SIZE 32
__global__ void kernel4(float * buf, int * indexbuf)
{
float a[ARRAY_SIZE];
...
int index = indexbuf[threadIdx.x + blockIdx.x * blockDim.x];
float val = a[index];
...
}
The number of load instruction replays can vary widely depending on the data in indexbuf:
- zero replays when
indexhas the same value for all threads of a warp; - Approximately 2.5 replays on average when
indexis an independent random variable with uniform distribution from 0 to 31; and - as high as 31 replays when
indexis different for all threads of a warp.
In this situation, a kernel might have so many local memory load and store replays that its performance drops significantly.
Fortunately there is a trick that can help you solve this problem. Let’s store the private array explicitly in shared memory!
Shared memory has 32 banks that are organized such that successive 32-bit words map to successive banks (see the CUDA C Programming Guide for details). For our example we’ll allocate a __shared__ array large enough to hold the private arrays of all threads of a threadblock.
We’ll logically assign elements of this new __shared__ array to the threads of the thread block so that all elements of our new virtual private array for each thread are stored in its own shared memory bank.
I will use THREADBLOCK_SIZE to define the size of the thread block (this value should be evenly divisible by the warp size, 32). Here the first THREADBLOCK_SIZE elements of our shared memory array contain all 0-index elements of the private arrays for all threads of the thread block. The next THREADBLOCK_SIZE elements of the shared memory array contain all 1-index elements of the private arrays, and so on. This approach is illustrated in Figure 3.
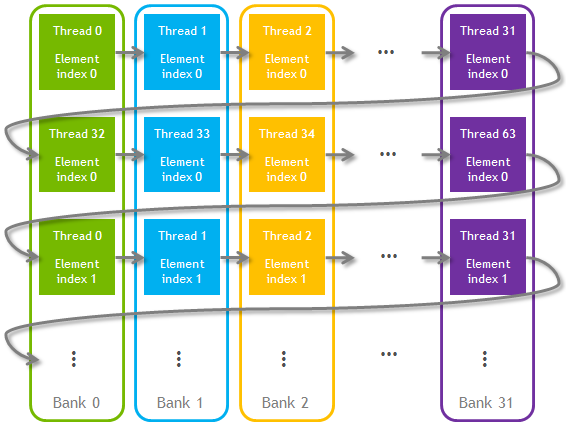
In this way we ensure that the whole virtual private array of thread 0 falls into shared memory bank 0, the array of thread 1 falls into bank 1, and so on. Thread 32—which is the first thread in the next warp—will occupy bank 0 again but there will be no shared memory bank conflicts with thread 0 (or any other bank 0 thread) since they belong to different warps and therefore will never read at the same instant.
The following code implements this idea.
// Should be multiple of 32
#define THREADBLOCK_SIZE 64
// Could be any number, but the whole array should fit into shared memory
#define ARRAY_SIZE 32
__device__ __forceinline__ int no_bank_conflict_index(int thread_id,
int logical_index)
{
return logical_index * THREADBLOCK_SIZE + thread_id;
}
__global__ void kernel5(float * buf, int * index_buf)
{
// Declare shared memory array A which will hold virtual
// private arrays of size ARRAY_SIZE elements for all
// THREADBLOCK_SIZE threads of a threadblock
__shared__ float A[ARRAY_SIZE * THREADBLOCK_SIZE];
...
int index = index_buf[threadIdx.x + blockIdx.x * blockDim.x];
// Here we assume thread block is 1D so threadIdx.x
// enumerates all threads in the thread block
float val = A[no_bank_conflict_index(threadIdx.x, index)];
...
}
As long as array A is declared __shared__, each access to an element of A is a load from (LDS) or store to (STS) shared memory, see Figure 4.
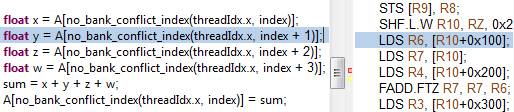
This technique guarantees that all accesses to this array (now located in shared memory) will execute without any replays. It’s possible to modify the code to eliminate the limitation to one-dimensional thread blocks with THREADBLOCK_SIZE divisible by 32.
This method has intrinsic limitations, though, associated with its use of shared memory. As the size of your array (located in shared memory) grows the occupancy drops. If the occupancy drops too low, performance may drop when the kernel has insufficient occupancy to hide latency. At some point this array will not fit into shared memory and you will not be able to run the kernel. 48 KB is the maximum shared memory size a thread block can use. In short, this method works for relatively small private arrays: up to 30-50 32-bit elements per thread.
Performance
For performance comparison I used a kernel with dynamic indexing of a private array of 32 32-bit elements. The kernel performance is limited by how fast it can access those elements.
I compared performance for 3 cases on an NVIDIA Tesla K20 accelerator:
- Uniform dynamic indexing, with private arrays stored in local memory.
- Non-uniform dynamic indexing with a worst-case access pattern that results in 31 replays, and private arrays stored in local memory.
- Non-uniform dynamic indexing with the same worst-case access pattern, but with private arrays stored in shared memory.
With private arrays stored in local memory, non-uniform indexing is, as we expect, much worse: 24x slower for my particular kernel. The interesting part is that a shared-memory-based kernel with non-uniform indexing is 1.34x faster than the local-memory-based kernel with uniform indexing, as Figure 5 shows.
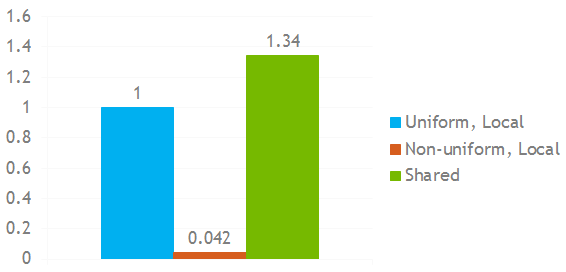
There is a good reason for this effect: the local memory version spills from the L1 cache to the L2 cache and even to global memory, while the shared memory version is able to fit all of the private arrays without any spilling.
Even for this kernel the relative performance depends on the architecture of the GPU. For example, on Maxwell the difference between the two local memory based cases is smaller—about 14x—but the shared memory version runs 4x faster than the local memory version with uniform indexing. Your particular kernel will more than likely behave differently, due to different instruction mix. Try it.
Summary
The performance of CUDA kernels that access private arrays can depend a lot on access patterns.
- Highest performance is achieved with uniform access when the compiler can derive constant indices for all accesses to the elements of the array, because the compiler will place elements of the array directly into registers.
- Uniform access with truly dynamic indexing causes the compiler to use local memory for the array. If 1) you have sufficient math instructions in the kernel to hide local load/store latency and 2) private arrays fit into L2/L1 caches, then the performance hit due to these additional loads/stores should be small.
- With non-uniform access, the cost depends on the number of unique elements addressed by each warp. In some cases the number of instruction replays can be very high.
- You can put small private arrays into shared memory and get zero replays (as in the uniform access case with dynamic indexing). This can help even if you had zero replays to start with because shared memory accesses are more “deterministic”, they don’t spill to L2 cache or global memory.