Graphs are mathematical structures used to model many types of relationships and processes in physical, biological, social and information systems. They are also used in the solution of various high-performance computing and data analytics problems. The computational requirements of large-scale graph processing for cyberanalytics, genomics, social network analysis and other fields demand powerful and efficient computing performance that only accelerators can provide. With CUDA 8, NVIDIA is introducing nvGRAPH, a new library of GPU-accelerated graph algorithms. Its first release, nvGRAPH 1.0, supports 3 key graph algorithms (PageRank, Single-Source Shortest Path, and Single-Source Widest Path), and our engineering and research teams are already developing new parallel algorithms for future releases. I’ll discuss one of them in detail in this blog post.
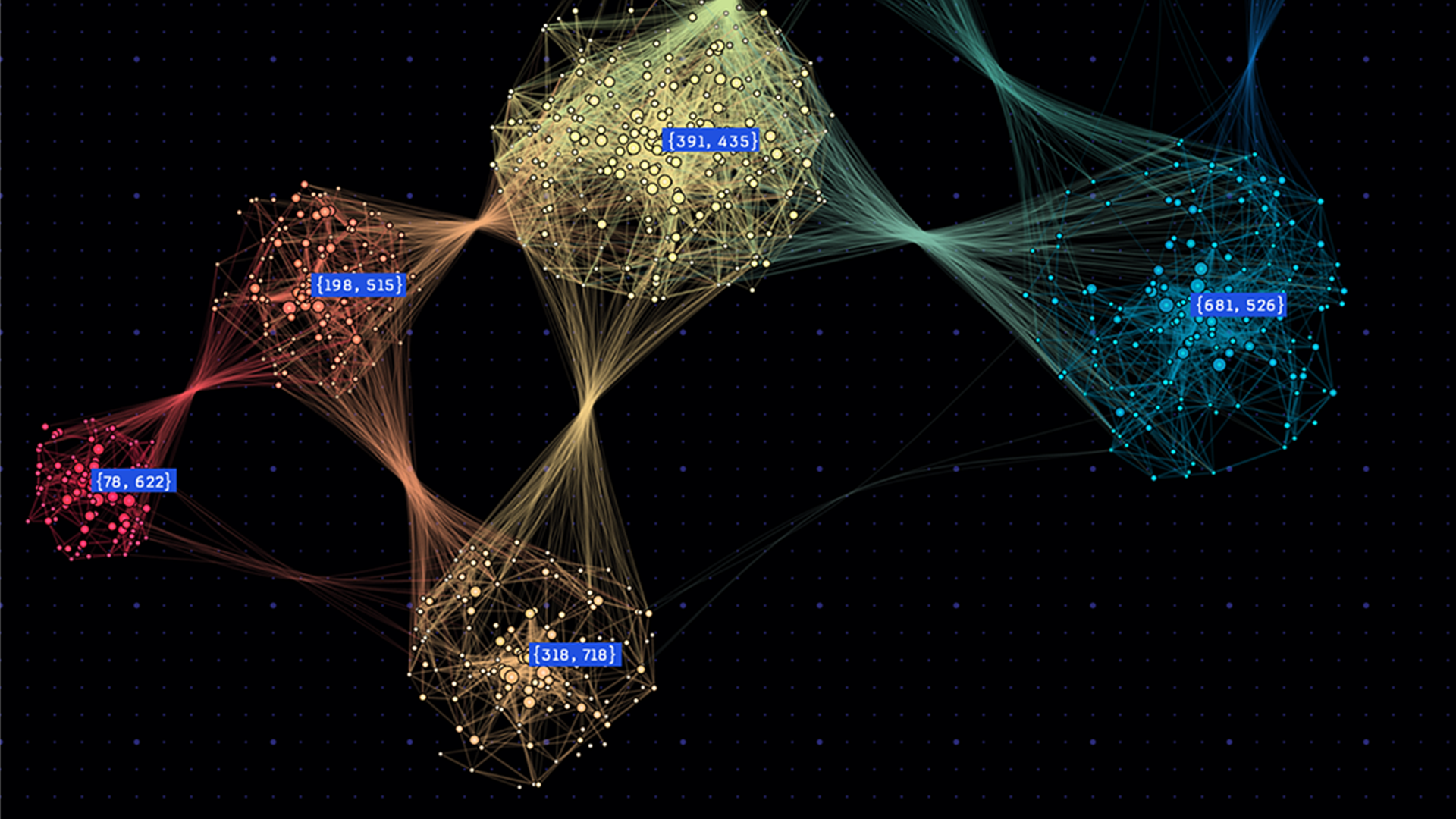
Many applications need to partition graphs into subgraphs, or to find clusters within them. For example, graph partitioning can be used in the numerical solution of partial differential equations (PDEs) to perform more efficient sparse matrix-vector multiplications, and graph clustering can be used to identify communities in social networks and for cybersecurity (see Figure 1).

The quality of graph partitioning or clustering can have a significant impact on the overall performance of an application. Therefore it is very important not only to find the splitting into subgraphs fast by taking advantage of GPUs (our GPU spectral graph partitioning scheme performs up to 7x faster than a CPU implementation), but also to find the best possible splitting, which requires development of new algorithms.
Also, graph partitioning and clustering aims to find a splitting of a graph into subgraphs based on a specific metric. In particular, spectral graph partitioning and clustering relies on the spectrum—the eigenvalues and associated eigenvectors—of the Laplacian matrix corresponding to a given graph. Next, I will formally define this problem, show how it is related to the spectrum of the Laplacian matrix, and investigate its properties and tradeoffs.
Definition
Let a graph be defined by its vertex set
and edge set
. The vertex set
represents
nodes in a graph, with each node identified by a unique integer number
. The edge set
represents
edges in a graph, with each edge from node
to
identified by a pair
.
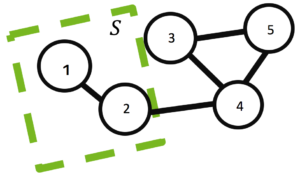
Applications often need to find a splitting of the graph into subgraphs of similar size connected by as few edges as possible. This statement is often formulated as the problem of finding a set of vertices that induces a minimum balanced cut of a graph
in the sense of a cost function
where denotes complement of set
with respect to
,
denotes the cardinality (number of elements) of a set, and
denotes the boundary of a set.
For example, a minimum balanced cut of a graph , with
and
induced by a set of vertices
with
and boundary
is shown in Figure 2.
It is important to point out that both partitioning and clustering aim to split the original graph into multiple sub-graphs. However, in partitioning the number of partitions and often their size is fixed, while in clustering the fact that there are no partitions can be a result in itself [1]. Also, the optimality of the splitting can be measured by different cost functions, including modularity, betweenness centrality, or flow.
Cost Function
I will focus on the popular ratio and normalized cut cost functions, which are variations of the minimum balanced cut of a graph . The ratio and normalized cut cost functions are defined as
and
respectively, where set for
, the intersection of sets
for
, and
denotes the volume of a set, where
is the degree (number of edges) of node
.
These cost functions are simpler than they look. Notice that the numerator refers to the number of edges cut between partitions and the denominator is related to the number of elements assigned to a particular partition. For example, in distributed sparse matrix-vector multiplication, the numerator relates to the number of elements that must be sent between partitions and the denominator to the work done per partition, measured in terms of the number of rows in the former or number of non-zero elements in the latter equation.
Also, it turns out that it is possible to express these cost functions as
and
where tall matrix ,
is the identity matrix and
is the trace of a matrix (the sum of its diagonal elements). Here vectors
take only discrete values, with non-zeroes corresponding to indices in the set
, while
is the Laplacian matrix, which will be defined next.
Laplacian Matrix
The Laplacian matrix is defined as , where
is the adjacency matrix of the graph
and the diagonal matrix
, where vector
.
For example, the Laplacian matrix for the graph shown ing Figure 2 can be written
The Laplacian matrix has very interesting properties. To illustrate it, let the set as shown in Figure 2 and vector
be such that it has 1 at position
and zero otherwise. Then, I can express the cardinality
, volume
as well as the cardinality of the boundary
of the set
using the vector
and the Laplacian matrix
in the following way.
This illustrates why in the previous section I could express all the terms in the ratio and normalized cost functions in terms of vector and the Laplacian matrix
. A more detailed explanation is given in our technical report [2].
Key Idea of Spectral Scheme
Notice that obtaining the minimum of the cost function by finding the best non-zero discrete values for the vector is no easier than finding the best indices for the set
. The two formulations of the cost functions are equivalent and both are NP-hard problems.
The key idea of spectral partitioning and clustering is not to look for the discrete solution directly, but instead to do it in two steps.
First, relax the discrete constraints and let vector take real instead of discrete values. In this case, following the linear algebra Courant-Fischer theorem (sometimes referred to as the Min-Max theorem), the minimum of the cost function is obtained by the eigenvectors associated with the
smallest eigenvalues of the Laplacian matrix.
Second, map the obtained real values back to the discrete ones to find the solution of interest. This step can be done using simple heuristics, such as sorting and looking for a gap in the real values, or using more advanced multi-dimensional algorithms, such as the k-means algorithm. In the former case all real values in between gaps, while in the latter case all real values clustered around a particular centroid, will be assigned the same discrete value and therefore will belong to the same particular partition or cluster.
There is no guarantee that the two-step approach will find the best solution, but in practice it often finds a good enough approximation and works reasonably well.
Figure 3 provides a visual outline of the process and Algorithm 1 presents the algorithm in pseudocode.
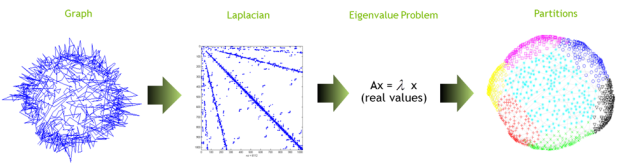
Let G=(V,E) be an input graph Let A be the adjacency matrix of G Let diagonal matrix D = diag(Ae) Set the Laplacian matrix L=D-A Solve the eigenvalue problem L u = λu Use heuristics to transform real into discrete values
Eigenvalue Problem
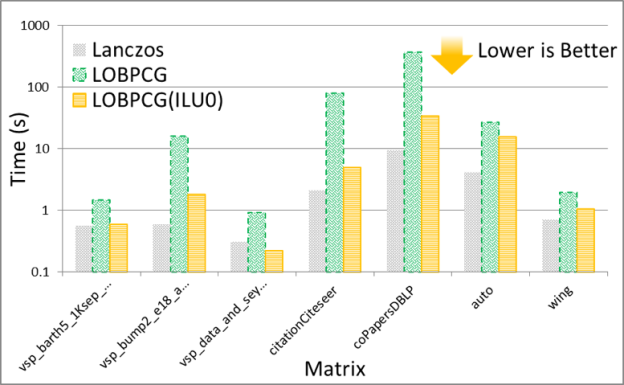
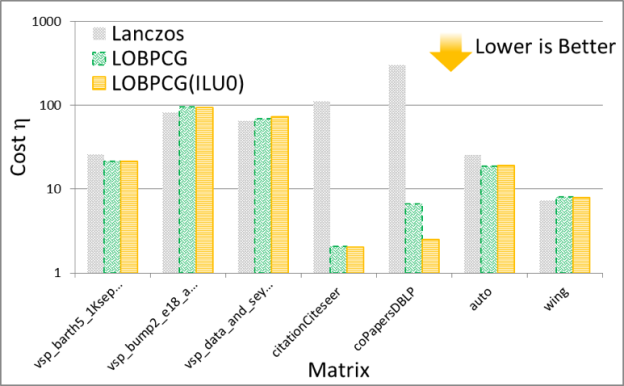
The solution of the eigenvalue problem is often the most time consuming part of spectral graph partitioning /clustering. There are many eigenvalue solvers that can be used to solve it, including Lanczos, Tracemin, Jacobi-Davidson and LOBPCG. In particular, Figures 3 and 4 show experimental results comparing the performance and quality, respectively, of the Lanczos and LOBPCG methods when looking for the 30 smallest eigenvectors of a few matrices from the DIMACS graph collection. Although Lanczos is often the fastest eigenvalue solver, when incomplete-LU with 0 fill-in (ILU0) is available, the preconditioned LOBPCG eigenvalue solver can be competitive and often computes a superior-quality solution.
Experiments
Now I’ll compare the spectral scheme on the GPU with the spectral scheme implemented on the CPU in the CHACO software package. The experiments are performed on a workstation with a 3.2 GHz Intel Core i7-3930K CPU and an NVIDIA Tesla K40c GPU.
The schemes are very similar, but not identical because CHACO has a slightly different implementation of the algorithms, and also attempts to provide a load-balanced cut within a fixed threshold , so that for instance
. Therefore, CHACO’s cost function is similar to the ratio cut, but the clustering at the end is biased towards providing a load-balanced partitioning, while still minimizing the edge cuts. Also, CHACO implements spectral bisection, so when comparing to it I split the graph into only two partitions.
Figures 5 and 6 show the performance and quality of both spectral schemes, respectively. Notice that the GPU spectral scheme using Lanczos often obtains the solution faster, but with variable quality compared to the CPU spectral scheme in CHACO, which also uses a variation of the Lanczos method. On the other hand when using preconditioned LOBPCG the GPU implementation is usually faster, and most of the time obtains a higher quality solution as measured by the cost functions. The detailed results of these experiments can be found in our technical report [2].
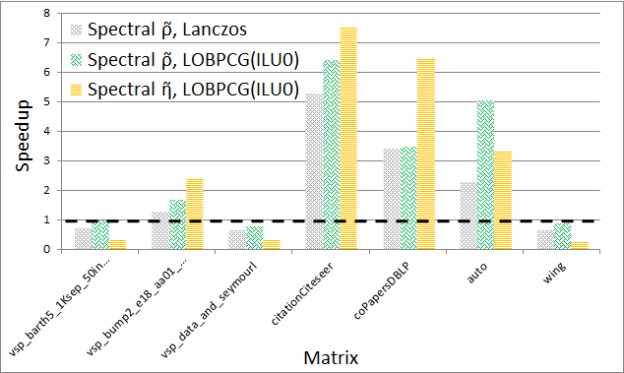
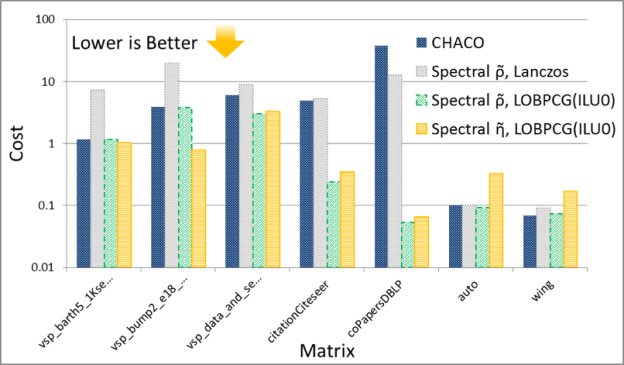
Finally, as mentioned earlier there exist many different partitioning and clustering strategies. In particular, some of the popular approaches for providing a balanced cut of a graph use multi-level schemes, implemented in software packages such as METIS. Both spectral and multi-level schemes are global methods that work on the entire graph, in contrast to local heuristics, such as the Kernighan-Lin algorithm.
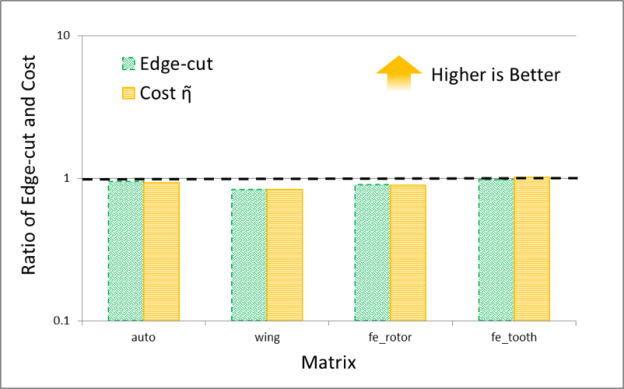
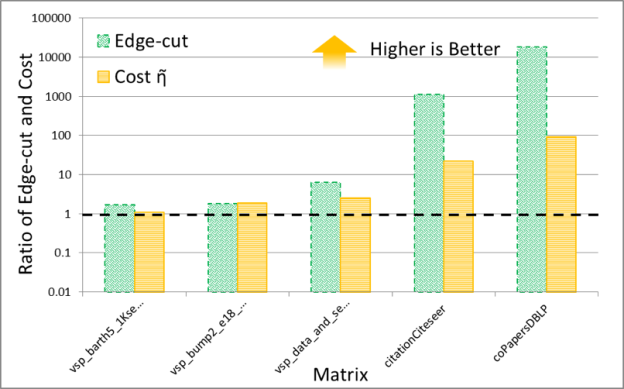
It is interesting to compare the quality of spectral and multi-level schemes in terms of the the edge-cut and cost function obtained by them. The numerical experiments shown in Figures 7 and 8 plot the ratio of these quantities (the cost obtained by METIS divided by the cost obtained by the GPU spectral scheme), for 30 partitions. The result trends indicate that the behavior of the spectral and multi-level schemes is starkly different for two classes of problems: (i) meshes arising from discretization of PDEs and (ii) social network graphs that often have power-law-like distributions of edges per node. My conjecture is that the difference in quality between these schemes results from the fact that multi-level schemes often rely on local information to construct a graph hierarchy that is used to partition the graph.
Notice that for PDEs the quality of the partitioning obtained by both schemes is essentially the same, while for networks with high degree nodes, such as social networks, spectral schemes can obtain significantly higher quality partitions. Even though in our experiments the time taken by the spectral schemes is often larger than that taken by the multi-level schemes, I think that spectral schemes can be a good choice in applications where quality is important. For example, in sparse linear algebra applications, even modest improvements in the quality of partitioning can lead to a significant impact on the overall application performance, so the extra partitioning cost of a spectral scheme may be worthwhile.
Conclusion
I hope that after reading this blog post you have learned some of the intuition behind the spectral graph partitioning/clustering scheme and how it compares to other similar algorithms. A more formal treatment of the subject, with precise derivation of the theoretical results and detailed numerical experiments, can be found in our technical report [2].
The numerical experiments show that spectral partitioning on GPUs can outperform spectral partitioning on the CPU by up to 7x. Also, it is clear that multi-level schemes are a good choice for partitioning meshes arising from PDEs, while spectral schemes can achieve high quality partitioning and clustering on network graphs with high-degree nodes, such as graphs of social networks.
If you need to accelerate graph algorithms in your applications, check out the new GPU-accelerated nvGRAPH library. You can also read more about nvGRAPH in the post “CUDA 8 Features Revealed”. We are considering adding spectral partitioning to nvGRAPH in the future. Please let us know in the comments if you would find this useful.
A Note on Drawing Graphs
Finally, note that eigenvectors of the Laplacian matrix have many other applications. For example, they can be used for drawing graphs. In fact, the graph drawings in this blog were done with them. The interpretation of eigenvectors for this application has been studied in [3].
References
[1] M.E.J. Newman, “Modularity and Community Structure in Networks”, Proc. National Academy of Science, Vol. 103, pp. 8577–8582, 2006.
[2] M. Naumov and T. Moon, “Parallel Spectral Graph Partitioning”, NVIDIA Research Technical Report, NVR-2016-001, March, 2016.
[3] Y. Koren, “Drawing Graphs by Eigenvectors: Theory and Practice”, Computers & Mathematics with Applications, Vol. 49, pp. 1867–1888, 2005.