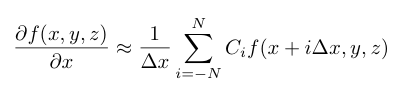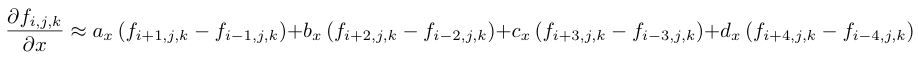In the previous CUDA C/C++ post we investigated how we can use shared memory to optimize a matrix transpose, achieving roughly an order of magnitude improvement in effective bandwidth by using shared memory to coalesce global memory access. The topic of today’s post is to show how to use shared memory to enhance data reuse in a finite difference code. In addition to shared memory, we will also discuss constant memory, which is a cached read-only memory optimized for uniform access across threads in a block (or warp).
In the previous CUDA C/C++ post we investigated how we can use shared memory to optimize a matrix transpose, achieving roughly an order of magnitude improvement in effective bandwidth by using shared memory to coalesce global memory access. The topic of today’s post is to show how to use shared memory to enhance data reuse in a finite difference code. In addition to shared memory, we will also discuss constant memory, which is a cached read-only memory optimized for uniform access across threads in a block (or warp).
Problem Statement: 3D Finite Difference
Our example uses a three-dimensional grid of size 643. For simplicity we assume periodic boundary conditions and only consider first-order derivatives, although extending the code to calculate higher-order derivatives with other types of boundary conditions is straightforward.
The finite difference method essentially uses a weighted summation of function values at neighboring points to approximate the derivative at a particular point. For a (2N+1)-point stencil with uniform spacing ∆x in the x direction, the following equation gives a central finite difference scheme for the derivative in x. Equations for the other directions are similar.
The coefficients Ci are typically generated from Taylor series expansions and can be chosen to obtain a scheme with desired characteristics such as accuracy, and in the context of partial differential equations, dispersion and dissipation. For explicit finite difference schemes such as the type above, larger stencils typically have a higher order of accuracy. For this post we use a nine-point stencil which has eighth-order accuracy. We also choose a symmetric stencil, shown in the following equation.
Here we specify values of the function on the computational grid using the grid indices i, j, k, rather than the physical coordinates x, y, z. Here the coefficients are ax = 4/(5 ∆x) , bx = −1/(5 ∆x) , cx = 4/(105 ∆x), and dx = − 1/(280 ∆x), which is a typical eighth-order scheme. For derivatives in the y and z directions, the index offsets in the above equation are simply applied to the j and k indices and the coefficients are the same except that ∆y and ∆z are used in place of ∆x.
Because we calculate an approximation to the derivative at each point on the 643 periodic grid, the value of f at each point is used eight times: once for each right-hand-side term in the above expression. In designing a derivative kernel, our goal is to exploit this data reuse by storing blocks of data in shared memory to ensure we fetch the values of f from global memory as few times as possible.
Data Reuse and Shared Memory
We employ a tiling approach in which each thread block loads a tile of data from the multidimensional grid into shared memory, so that each thread in the block can access all elements of the shared memory tile as needed. How do we choose the best tile shape and size? Some experimentation is required, but characteristics of the finite difference stencil and grid size provide direction.
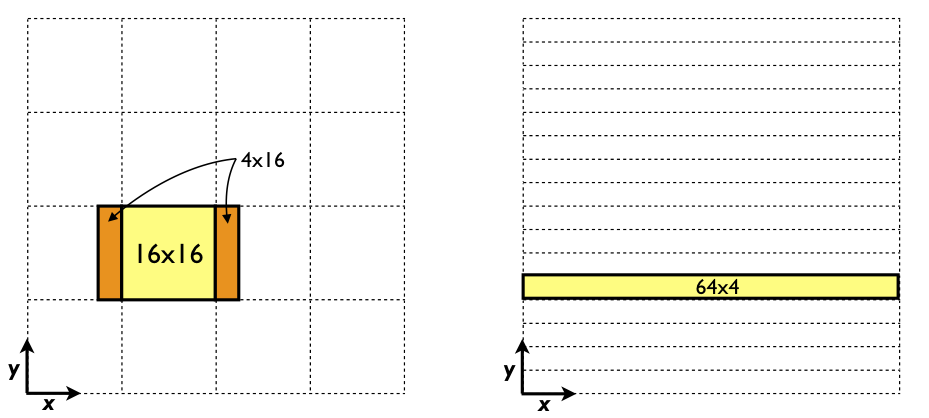
When choosing a tile shape for stencil calculations, the tiles typically overlap by half of the stencil size, as depicted on the left in the figure below.
Here, in order to calculate the derivative in a 16 × 16 tile (in yellow), the values of f not only from this tile but also from two additional 4 × 16 sections (in orange) must be loaded by each thread block. Overall, the f values in the orange sections get loaded twice, once by the thread block that calculates the derivative at that location, and once by each neighboring thread block. As a result, 8 × 16 values out of 16 × 16, or half of the values, get loaded from global memory twice. In addition, coalescing on devices with a compute capability of 2.0 and higher will be suboptimal with 16 × 16 tiles because perfect coalescing on such devices requires access to data within 32 contiguous elements in global memory per load.
A better choice of tile (and thread block) size for our problem and data size is a 64 × 4 tile, as depicted on the right in the figure above. This tile avoids overlap altogether when calculating the x-derivative for our one-dimensional stencil on a grid of 643 since the tile contains all points in the direction of the derivative. A minimal tile would have just one pencil, or one-dimensional array of all points in a direction. This would correspond to thread blocks of only 64 threads, however, so from an occupancy standpoint it is beneficial to use multiple pencils per tile. In our finite difference code, available for download on Github, we parameterize the number of pencils to allow experimentation. In addition to loading each value of f only once, every warp of threads loads contiguous data from global memory using this tile and therefore achieves perfectly coalesced accesses to global memory.
X-Derivative Implementation
The implementation for the x-derivative kernel follows.
__global__ void derivative_x(float *f, float *df)
{
__shared__ float s_f[sPencils][mx+8]; // 4-wide halo
int i = threadIdx.x;
int j = blockIdx.x*blockDim.y + threadIdx.y;
int k = blockIdx.y;
int si = i + 4; // local i for shared memory access + halo offset
int sj = threadIdx.y; // local j for shared memory access
int globalIdx = k * mx * my + j * mx + i;
s_f[sj][si] = f[globalIdx];
__syncthreads();
// fill in periodic images in shared memory array
if (i < 4) {
s_f[sj][si-4] = s_f[sj][si+mx-5];
s_f[sj][si+mx] = s_f[sj][si+1];
}
__syncthreads();
df[globalIdx] =
( c_ax * ( s_f[sj][si+1] - s_f[sj][si-1] )
+ c_bx * ( s_f[sj][si+2] - s_f[sj][si-2] )
+ c_cx * ( s_f[sj][si+3] - s_f[sj][si-3] )
+ c_dx * ( s_f[sj][si+4] - s_f[sj][si-4] ) );
}
Here mx, my, and mz are the array dimensions which are set to 64, and sPencils is 4, which is the number of pencils used to make the shared memory tile. The indices i, j, and k correspond to the coordinates in the 643 mesh. The indices si and sj are the local (row, column) coordinates for the shared memory tile. This kernel is launched with a block of 64 × sPencils threads which calculate the derivatives on a x × y tile of 64 × sPencils elements, so each thread calculates the derivative at one point.
The shared memory tile is declared with a padding of 4 elements at each end of the x dimension to accommodate the periodic images needed to calculate the derivative at the endpoints.
__shared__ float s_f[sPencils][mx+8]; // 4-wide halo
We compute an index into the linear input array and then read from global memory into the shared memory tile.
int globalIdx = k * mx * my + j * mx + i; s_f[sj][si] = f[globalIdx];
These reads from global memory are perfectly coalesced. Data are copied within shared memory to fill out the periodic images in the x-direction by the following code.
// fill in periodic images in shared memory array
if (i < 4) {
s_f[sj][si-4] = s_f[sj][si+mx-5];
s_f[sj][si+mx] = s_f[sj][si+1];
}
Note that in this operation we are reading from shared memory, not from global memory. Each element is read from global memory only once by the previous statement. Since a thread reads data from shared memory that another thread wrote, we need a __syncthreads() call before the periodic images are written. Likewise, we need a __syncthreads() call after the periodic images are written since they are accessed by different threads. After the second __syncthreads() call, our finite difference approximation is calculated using the following code.
df[globalIdx] = ( c_ax * ( s_f[sj][si+1] - s_f[sj][si-1] ) + c_bx * ( s_f[sj][si+2] - s_f[sj][si-2] ) + c_cx * ( s_f[sj][si+3] - s_f[sj][si-3] ) + c_dx * ( s_f[sj][si+4] - s_f[sj][si-4] ) );
The coefficients c_ax, c_bx, c_cx, and c_dx are declared external to this kernel in constant memory.
Constant memory
Constant memory is a special-purpose memory space that is read-only from device code, but can be read and written by the host. Constant memory resides in device DRAM, and is cached on chip. The constant memory cache has only one read port, but can broadcast data from this port across a warp. This means that constant memory access is effective when all threads in a warp read the same address, but when threads in a warp read different addresses the reads are serialized. Constant memory is perfect for coefficients and other data that are used uniformly across threads, as is the case with our coefficients c_ax, c_bx, etc.
In CUDA C/C++, constant data must be declared with global scope, and can be read (only) from device code, and read or written by host code. Constant memory is used in device code the same way any CUDA C variable or array/pointer is used, but it must be initialized from host code using cudaMemcpyToSymbol or one of its variants. In our finite difference code we have the following constant declarations, which use the __constant__ declaration specifier.
// stencil coefficients __constant__ float c_ax, c_bx, c_cx, c_dx; __constant__ float c_ay, c_by, c_cy, c_dy; __constant__ float c_az, c_bz, c_cz, c_dz;
We initialize the x coefficients using the following code, and the y and z coefficients are initialized similarly.
// stencil weights (for unit length problem) float dsinv = mx-1.f; float ax = 4.f / 5.f * dsinv; float bx = -1.f / 5.f * dsinv; float cx = 4.f / 105.f * dsinv; float dx = -1.f / 280.f * dsinv; cudaMemcpyToSymbol(c_ax, &ax, sizeof(float), 0, cudaMemcpyHostToDevice); cudaMemcpyToSymbol(c_bx, &bx, sizeof(float), 0, cudaMemcpyHostToDevice); cudaMemcpyToSymbol(c_cx, &cx, sizeof(float), 0, cudaMemcpyHostToDevice); cudaMemcpyToSymbol(c_dx, &dx, sizeof(float), 0, cudaMemcpyHostToDevice);
X Derivative Performance
The derivative_x kernel achieves the following performance on a Tesla K20c GPU.
Using shared memory tile of 64 x 4 RMS error: 7.277675e-06 MAX error: 2.861023e-05 Average time (ms): 0.025912 Average Bandwidth (GB/s): 80.933625
We will use this performance as a basis for comparison for derivatives in the other directions, which we will cover in the next CUDA C/C++ post.