![]() Numba is an open-source just-in-time (JIT) Python compiler that generates native machine code for X86 CPU and CUDA GPU from annotated Python Code. (Mark Harris introduced Numba in the post Numba: High-Performance Python with CUDA Acceleration.) Numba specializes in Python code that makes heavy use of NumPy arrays and loops. In addition to JIT compiling NumPy array code for the CPU or GPU, Numba exposes “CUDA Python”: the CUDA programming model for NVIDIA GPUs in Python syntax.
Numba is an open-source just-in-time (JIT) Python compiler that generates native machine code for X86 CPU and CUDA GPU from annotated Python Code. (Mark Harris introduced Numba in the post Numba: High-Performance Python with CUDA Acceleration.) Numba specializes in Python code that makes heavy use of NumPy arrays and loops. In addition to JIT compiling NumPy array code for the CPU or GPU, Numba exposes “CUDA Python”: the CUDA programming model for NVIDIA GPUs in Python syntax.
By speeding up Python, we extend its ability from a glue language to a complete programming environment that can execute numeric code efficiently.
From Prototype to Full Dataset with @cuda.jit
When doing exploratory programming, the interactivity of IPython Notebook and a comprehensive collection of scientific libraries (e.g. SciPy, Scikit-Learn, Theano, etc.) allow data scientists to process and visualize their data quickly. There are times when a fast implementation of what you need isn’t in a library, and you have to implement something new. Numba helps by letting you write pure Python code and run it with speed comparable to a compiled language, like C++. Your development cycle shortens when your prototype Python code can scale to process the full dataset in a reasonable amount of time.
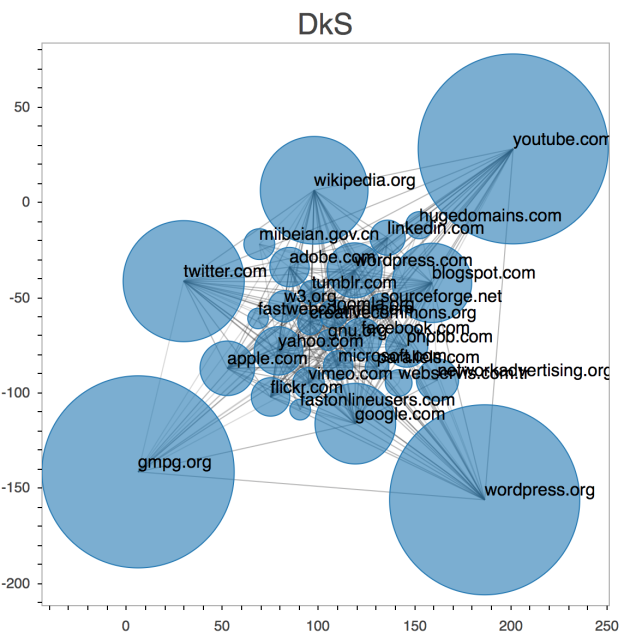
Working with Dr. Alex Dimakis and his team at UT Austin, we implemented their densest-k-subgraph (DkS) algorithm [1]. Our goal was to extract the densest domain from the 2012 WebDataCommon pay-level-domain hyperlink graph using one NVIDIA Tesla K20 GPU accelerator. We developed the entire application using NumPy for array operations, Numba to JIT compile Python to CUDA, pyculib for GPU sorting and cuBLAS routines, and Bokeh for plotting the results.
Figure 1 shows an example of the DkS result of the 2012 paylevel domain (plot created with Bokeh).
Part of the DkS code is an eigen-decomposition on the hyperlink graph to produce a low-rank approximation, which is equivalent to a PageRank. We chose the random walk algorithm by Sarma, Atish Das, et al. [2] due to its low communication overhead. Our previous attempt used power iteration and cuBLAS for matrix-vector multiplication, but the high demand on global memory traffic made it impossible to scale to the full graph.
Random Walk Densest-K-Subgraph Algorithm
The random walk algorithm works as follows: Initially, every node has a fixed number of coupons. At each round, coupons from each node are transferred to a randomly chosen connected node or are discarded with a small probability. The algorithm runs as long as there are coupons.
To perform the random selection on the GPU, we implemented the following simple 64-bit xorshift*.
@cuda.jit("(uint64[:], uint64)", device=True)
def cuda_xorshiftstar(states, id):
x = states[id]
x ^= x >> 12
x ^= x << 25 x ^= x >> 27
states[id] = x
return uint64(x) * uint64(2685821657736338717)
The @cuda.jit decorator tells Numba to compile cuda_xorshiftstar as a CUDA __device__ function. The function can then be called in the actual CUDA random walk kernel. The majority of the work is in the following cuda_random_walk_per_node __device__ function.
@cuda.jit(device=True)
def cuda_random_walk_per_node(curnode, visits, colidx, edges, resetprob,
randstates):
tid = cuda.threadIdx.x
randnum = cuda_xorshiftstar_float(randstates, tid)
if randnum >= resetprob:
base = colidx[curnode]
offset = colidx[curnode + 1]
# If the edge list is non-empty
if offset - base > 0:
# Pick a random destination
randint = cuda_xorshiftstar(randstates, tid)
randdestid = (uint64(randint % uint64(offset - base)) +
uint64(base))
dest = edges[randdestid]
else:
# Random restart
randint = cuda_xorshiftstar(randstates, tid)
randdestid = randint % uint64(visits.size)
dest = randdestid
# Increment visit count
cuda.atomic.add(visits, dest, 1)
This function forwards each coupon to a randomly chosen connected node. If the current node has no outgoing edges, the coupon is forwarded to a random node.
Our GPU PageRank implementation completed in just 163 seconds on the full graph of 623 million edges and 43 million nodes using a single NVIDIA Tesla K20 GPU accelerator. Our equivalent Numba CPU-JIT version took at least 5 times longer on a smaller graph.
Visualizing the Code
During development, the ability to visualize what the algorithm is doing can help you understand the run-time code behavior and discover performance bottlenecks. Initially, the PageRank ran 7x slower than the final version. Since the algorithm works by randomly sending “visitors” to connected nodes, an inefficient work distribution can cause severe warp divergence. We plotted the visits per node as a heat map with Bokeh, as shown in Figure 2.
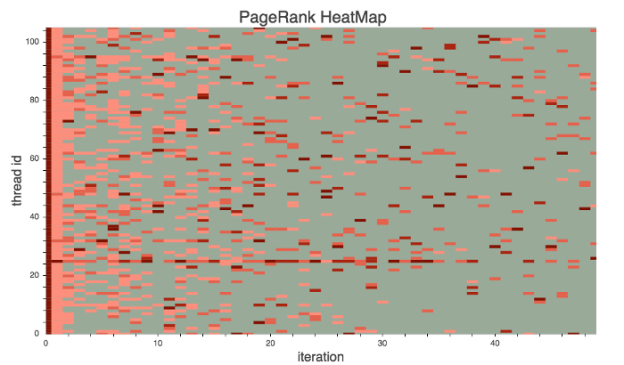
From the plot, we could see that the work was randomly distributed, resulting in severe load imbalance and high thread divergence. Figure 3 clearly shows the effect of our optimizations.
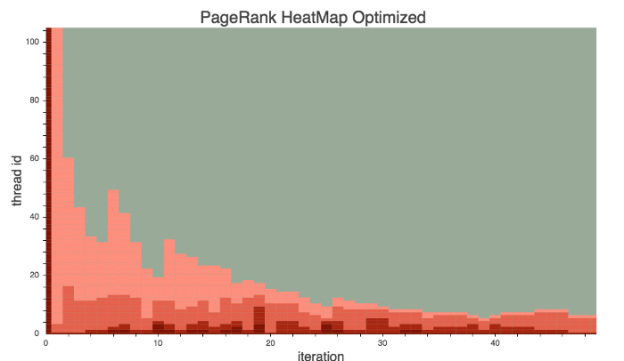
We implemented two main optimizations. First, we applied reference indirection. The original code randomly distributed coupons to nodes, and each thread handled one node. To improve this, we created an indirection table that maps each thread’s index threadIdx to node indices, instead of directly using threadIdx as the node index. We sorted the table entries in descending order of coupon count. This ensured that nodes of similar coupon count were next to each other. This reduced warp divergence, but the improvement was limited.
The optimization that made the difference was changing the work distribution and scheduling. Instead of assigning each thread to handle one node, we assigned blocks so that each block dynamically scheduled threads to work on each coupon. This added the following small boilerplate code to the kernel.
tid = cuda.threadIdx.x
while coupon_count > 0:
if tid < coupon_count:
do_work(...)
coupon_count -= min(coupon_count, cuda.blockDim.x)
We kept the reference redirection because the sorted array of coupons allows us to easily determine the last blockIdx that has nonzero coupons. As a result, the grid size can be adjusted at each round to launch exactly as many blocks as there are active nodes (nodes with non-zero coupon count). This resolved the warp divergence problem and avoided launching unnecessary blocks, increasing overall device utilization.
As a bonus, here’s another example of interactive development. It contains code we used during the development of a customized spring-layout algorithm to visualize the DkS graph. This allowed us to quickly discover bugs and fine tune parameters for the algorithm. This example uses Numba to JIT compile part of the layout physics to make the animation more fluid (it does not use the GPU, however).
Get Started with Numba Today
Numba provides Python developers with an easy entry into GPU-accelerated computing and a path for using increasingly sophisticated CUDA code with a minimum of new syntax and jargon. You can start with simple function decorators to automatically compile your functions, or use the powerful CUDA libraries exposed by pyculib. As you advance your understanding of parallel programming concepts and when you need expressive and flexible control of parallel threads, CUDA is available without requiring you to jump in on the first day.
Numba is a BSD-licensed, open source project which itself relies heavily on the capabilities of the LLVM compiler. The GPU backend of Numba utilizes the LLVM-based NVIDIA Compiler SDK. The pyculibwrappers around the CUDA libraries are also open source and BSD-licensed.
To get started with Numba, the first step is to download and install the Anaconda Python distribution, a “completely free enterprise-ready Python distribution for large-scale data processing, predictive analytics, and scientific computing” that includes many popular packages (Numpy, Scipy, Matplotlib, iPython, etc) and “conda”, a powerful package manager. Once you have Anaconda installed, install the required CUDA packages by typing conda install numba cudatoolkit pyculib. Then check out the Numba tutorial for CUDA on the ContinuumIO github repository. I also recommend that you check out the Numba posts on Anaconda’s blog.
[1] Papailiopoulos, Dimitris, et al. “Finding dense subgraphs via low-rank bilinear optimization.” Proceedings of the 31st International Conference on Machine Learning (ICML-14). 2014.
[2] Sarma, Atish Das, et al. “Fast distributed PageRank computation.” Theoretical Computer Science 561 (2015): 113-121.