In the previous two posts we looked at how to move data efficiently between the host and device. In this sixth post of our CUDA Fortran series we discuss how to efficiently access device memory, in particular global memory, from within kernels.
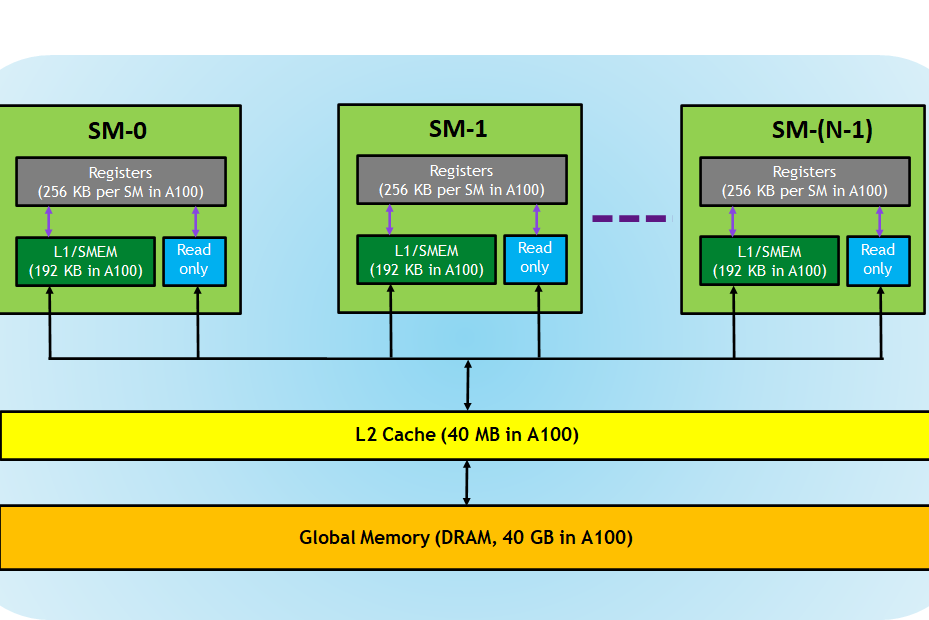
There are several kinds of memory on a CUDA device, each with different scope, lifetime, and caching behavior. So far in this series we have used global memory, which resides in device DRAM, for transfers between the host and device as well as for the data input to and output from kernels. The name global here refers to scope, as it can be accessed and modified from both the host and the device. Global memory is declared in host code via the device variable attribute and can persist for the lifetime of the application. Depending on the compute capability of the device, global memory may or may not be cached on the chip.
Before we go into how global memory is accessed, we need to refine our understanding of the CUDA execution model. We have discussed how threads are grouped into thread blocks, which are assigned to multiprocessors on the device. During execution there is a finer grouping of threads into groups of threads called warps. Multiprocessors on the GPU execute instructions for each warp in SIMD (Single Instruction Multiple Data) fashion. The warp size (effectively the SIMD width) of all current CUDA-capable GPUs is 32 threads.
Global Memory Coalescing
Grouping of threads into warps is not only relevant to computation, but also to global memory accesses. The device coalesces global memory loads and stores issued by threads of a warp into as few transactions as possible in order to minimize DRAM bandwidth (on older hardware of compute capability less than 2.0, transactions are coalesced within half warps of 16 threads rather than whole warps). To elucidate the conditions under which coalescing occurs across CUDA device architectures we run some simple experiments on three Tesla cards: a Tesla C870 (compute capability 1.0), a Tesla C1060 (compute capability 1.3), and a Tesla C2050 (compute capability 2.0).
We run two experiments that use variants of an increment kernel shown in the following code, one with an array offset that can cause misaligned accesses to the input array, and the other with strided accesses to the input array.
module kernels_m
integer, parameter :: singlePrecision = kind(0.0)
integer, parameter :: doublePrecision = kind(0.0d0)
integer, parameter :: fp_kind = singlePrecision
contains
attributes(global) subroutine offset(a, s)
real (fp_kind) :: a(*)
integer, value :: s
integer :: i
i = blockDim%x*(blockIdx%x-1)+threadIdx%x + s
a(i) = a(i)+1
end subroutine offset
attributes(global) subroutine stride(a, s)
real (fp_kind) :: a(*)
integer, value :: s
integer :: i
i = 1 + (blockDim%x*(blockIdx%x-1)+threadIdx%x-1) * s
a(i) = a(i)+1
end subroutine stride
end module kernels_m
program offsetAndStride
use cudafor
use kernels_m
implicit none
integer, parameter :: nMB = 4 ! NB: a_d(33*nMB) for stride case
integer, parameter :: blockSize = 256
integer :: n
real (fp_kind), device, allocatable :: a_d(:)
type(cudaEvent) :: startEvent, stopEvent
type(cudaDeviceProp) :: prop
integer :: i, istat
real(4) :: time
istat = cudaGetDeviceProperties(prop, 0)
write(*,'(/,"Device: ",a)') trim(prop%name)
write(*,'("Transfer size (MB): ",i0)') nMB
if (kind(a_d) == singlePrecision) then
write(*,'(a,/)') 'Single Precision'
else
write(*,'(a,/)') 'Double Precision'
endif
n = nMB*1024*1024/fp_kind
allocate(a_d(n*33))
istat = cudaEventCreate(startEvent)
istat = cudaEventCreate(stopEvent)
write(*,*) 'Offset, Bandwidth (GB/s):'
call offset<<>>(a_d, 0)
do i = 0, 32
a_d = 0.0
istat = cudaEventRecord(startEvent,0)
call offset<<>>(a_d, i)
istat = cudaEventRecord(stopEvent,0)
istat = cudaEventSynchronize(stopEvent)
istat = cudaEventElapsedTime(time, startEvent, stopEvent)
write(*,*) i, 2*nMB/time*(1.e+3/1024)
enddo
write(*,*)
write(*,*) 'Stride, Bandwidth (GB/s):'
call stride<<>>(a_d, 1)
do i = 1, 32
a_d = 0.0
istat = cudaEventRecord(startEvent,0)
call stride<<>>(a_d, i)
istat = cudaEventRecord(stopEvent,0)
istat = cudaEventSynchronize(stopEvent)
istat = cudaEventElapsedTime(time, startEvent, stopEvent)
write(*,*) i, 2*nMB/time*(1.e+3/1024)
enddo
istat = cudaEventDestroy(startEvent)
istat = cudaEventDestroy(stopEvent)
deallocate(a_d)
end program offsetNStride
This code can run both offset and stride kernels in either single or double precision by changing the fp_kind parameter at the top of the code. Each kernel takes two arguments, an input array and an integer representing the offset or stride used to access the elements of the array. The kernels are called in loops over a range of offset and strides.
Misaligned Data Accesses
The results for the offset kernel on the Tesla C870, C1060, and C2050 are shown in the following figure.
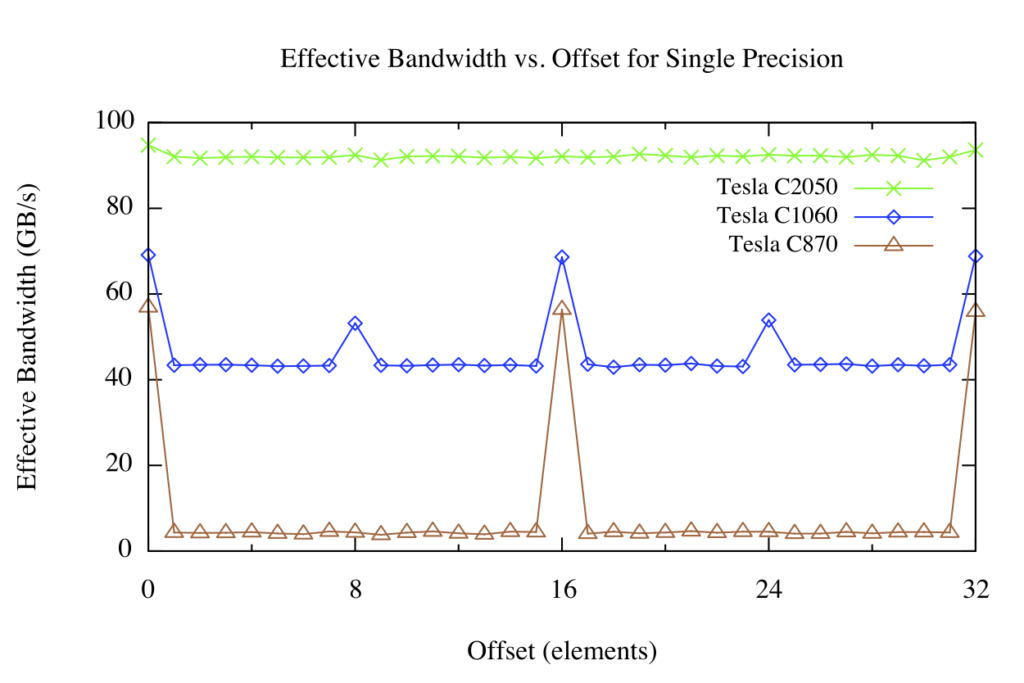
Arrays allocated (either explicitly or implicitly) in device memory, are aligned to 256-byte memory segments by the CUDA driver. The device can access global memory via 32-, 64-, or 128-byte transactions that are aligned to their size. For the C870 or any other device with a compute capability of 1.0, any misaligned access by a half warp of threads (or aligned access where the threads of the half warp do not access memory in sequence) results in 16 separate 32-byte transactions. Since only 4 bytes are requested per 32-byte transaction, one would expect the effective bandwidth to be reduced by a factor of eight, which is roughly what we see in the figure above (brown line) for offsets that are not a multiple of 16 elements, corresponding to one half warp of threads.
For the Tesla C1060 or other devices with compute capability of 1.2 or 1.3, misaligned accesses are less problematic. Basically, the misaligned accesses of contiguous data by a half warp of threads are serviced in a few transactions that “cover” the requested data. There is still a performance penalty relative to the aligned case due to both unrequested data being transferred and some overlap of data requested by different half-warps, but the penalty is far less than for the C870.
Devices of compute capability 2.0, such as the Tesla C2050, have an L1 cache in each multiprocessor with a 128-byte line size. Accesses by threads in a warp are coalesced into as few cache lines as possible, resulting in negligible effect of alignment on throughput for sequential memory accesses across threads.
Strided Memory Access
The results of the stride kernel are shown below:
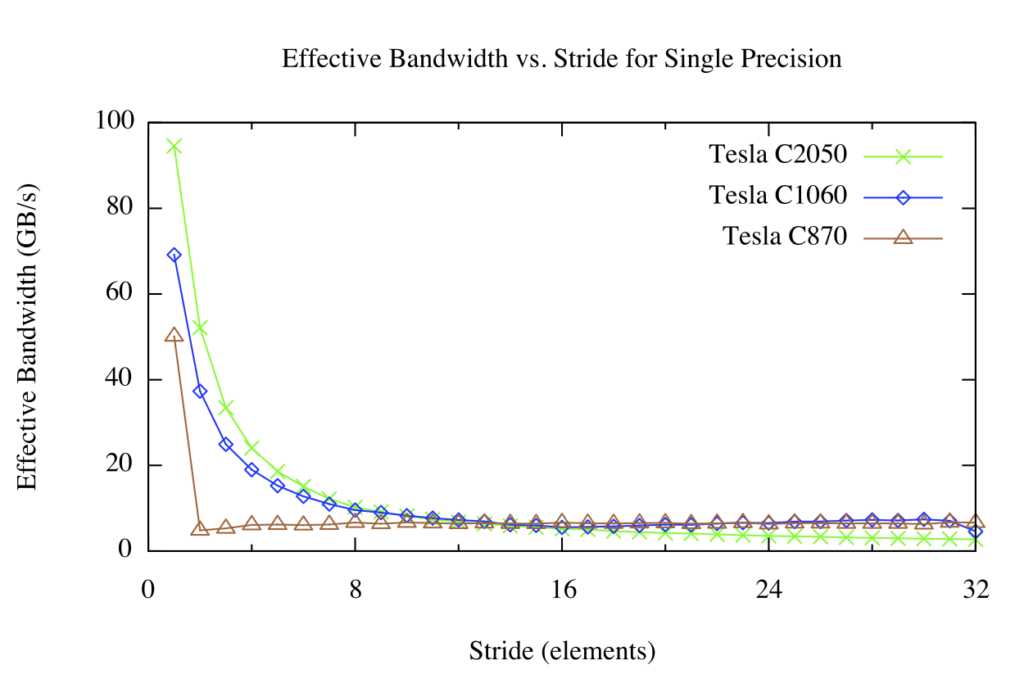
For strided global memory access we have a different picture. For large strides, the effective bandwidth is poor regardless of the version of the architecture. This should not be surprising: when concurrent threads simultaneously access memory addresses that are very far apart in physical memory, then there is no chance for the hardware to combine the accesses. You can see in the figure above that on the 870 that any stride other than 1 results in drastically reduced effective bandwidth. This is because compute capability 1.0 and 1.1 hardware requires linear, aligned accesses across threads for coalescing, so we see the familiar 1/8 bandwidth that we also saw in the offset kernel. Compute capability 1.2 and higher hardware can coalesce accesses that fall into aligned segments (32, 64, or 128 byte segments on CC 1.2/1.3, and 128-byte cache lines on CC 2.0 and higher), so this hardware results in a smooth bandwidth curve.
When accessing multidimensional arrays it is often necessary for threads to index the higher dimensions of the array, so strided access is simply unavoidable. We can handle these cases by using a type of CUDA memory called shared memory. Shared memory is an on-chip memory which is shared by all threads in a thread block. One use of shared memory is to extract a 2D tile of a multidimensional array from global memory in a coalesced fashion into shared memory, and then have contiguous threads stride through the shared memory tile. Unlike global memory, there is no penalty for strided access of shared memory. We will cover shared memory in detail in the next post.
Summary
In this post we discussed some aspects of how to efficiently access global memory from within CUDA kernel code. Global memory access on the device shares performance characteristics with data access on the host; namely, that data locality is very important. In early CUDA hardware, memory access alignment was as important as locality across threads, but on recent hardware alignment is not much of a concern. On the other hand, strided memory access can hurt performance, which can be alleviated using on-chip shared memory. In the next post we will explore shared memory in detail, and in the post after that we will show how shared memory can be used to avoid strided global memory accesses during a matrix transpose.