C++
Mar 06, 2024
How to Accelerate Quantitative Finance with ISO C++ Standard Parallelism
Quantitative finance libraries are software packages that consist of mathematical, statistical, and, more recently, machine learning models designed for use in...
10 MIN READ
Aug 08, 2023
Accelerate 3D Workflows with Modular, OpenUSD-Powered Omniverse Release
The latest release of NVIDIA Omniverse delivers an exciting collection of new features based on Omniverse Kit 105, making it easier than ever for developers to...
7 MIN READ
Apr 20, 2023
Debugging a Mixed Python and C Language Stack
Debugging is difficult. Debugging across multiple languages is especially challenging, and debugging across devices often requires a team with varying skill...
18 MIN READ
Mar 06, 2023
Maximizing Performance with Massively Parallel Hash Maps on GPUs
Decades of computer science history have been devoted to devising solutions for efficient storage and retrieval of information. Hash maps (or hash tables) are a...
19 MIN READ

Mar 02, 2023
New Course: Scaling GPU-Accelerated Applications with the C++ Standard Library
Learn how to write scalable GPU-accelerated hybrid applications using C++ standard language features alongside MPI in this interactive hands-on self-paced...
1 MIN READ
Jan 09, 2023
Rapidly Build AI-Streaming Apps with Python and C++
The computational needs for AI processing of sensor streams at the edge are increasingly demanding. Edge devices must keep up with high rates of incoming data...
5 MIN READ

Dec 19, 2022
New Course: GPU Acceleration with the C++ Standard Library
Learn how to write simple, portable, parallel-first GPU-accelerated applications using only C++ standard language features in this self-paced course from the...
1 MIN READ

Jul 26, 2022
Accelerating GPU Applications with NVIDIA Math Libraries
There are three main ways to accelerate GPU applications: compiler directives, programming languages, and preprogrammed libraries. Compiler directives such as...
12 MIN READ

May 31, 2022
Improve Guidance and Performance Visualization with the New Nsight Compute
NVIDIA Nsight Compute is an interactive kernel profiler for CUDA applications. It provides detailed performance metrics and API debugging through a user...
3 MIN READ
Feb 24, 2022
Speeding up Numerical Computing in C++ with a Python-like Syntax in NVIDIA MatX
Rob Smallshire once said, "You can write faster code in C++, but write code faster in Python." Since its release more than a decade ago, CUDA has given C and...
6 MIN READ

Nov 10, 2021
NVIDIA GTC: A Complete Overview of Nsight Developer Tools
The Nsight suite of Developer Tools provide insightful tracing, debugging, profiling, and other analyses to optimize your complex computational applications...
6 MIN READ

Aug 10, 2021
Announcing Nsight Deep Learning Designer 2021.1 - A Tool for Efficient Deep Learning Model Design and Development
Nsight Deep Learning Designer 2021.1 Today NVIDIA announced Nsight DL Designer - the first in-class integrated development environment to support efficient...
3 MIN READ
Mar 10, 2021
NVIDIA Tools Extension API: An Annotation Tool for Profiling Code in Python and C/C++
As PyData leverages much of the static language world for speed including CUDA, we need tools which not only profile and measure across languages but also...
9 MIN READ
Dec 08, 2020
Fast, Flexible Allocation for NVIDIA CUDA with RAPIDS Memory Manager
When I joined the RAPIDS team in 2018, NVIDIA CUDA device memory allocation was a performance problem. RAPIDS cuDF allocates and deallocates memory at high...
24 MIN READ
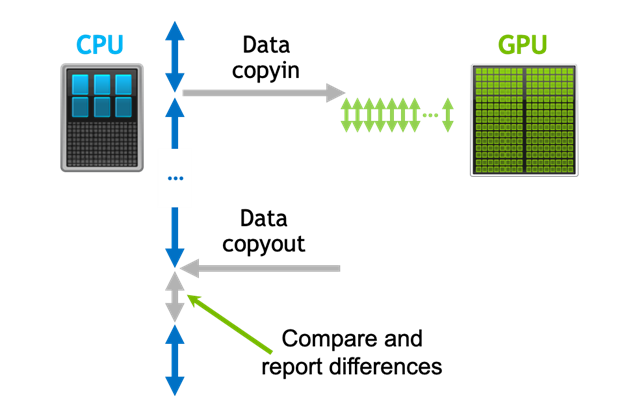
Nov 18, 2020
Detecting Divergence Using PCAST to Compare GPU to CPU Results
Parallel Compiler Assisted Software Testing (PCAST) is a feature available in the NVIDIA HPC Fortran, C++, and C compilers. PCAST has two use cases. The first...
14 MIN READ

Aug 04, 2020
Accelerating Standard C++ with GPUs Using stdpar
Historically, accelerating your C++ code with GPUs has not been possible in Standard C++ without using language extensions or additional libraries: CUDA C++...
19 MIN READ