CUDA C++

Nov 13, 2023
Simplifying GPU Programming for HPC with NVIDIA Grace Hopper Superchip
The new hardware developments in NVIDIA Grace Hopper Superchip systems enable some dramatic changes to the way developers approach GPU programming. Most...
17 MIN READ
Aug 22, 2023
Simplifying GPU Application Development with Heterogeneous Memory Management
Heterogeneous Memory Management (HMM) is a CUDA memory management feature that extends the simplicity and productivity of the CUDA Unified Memory programming...
16 MIN READ
Apr 20, 2023
Debugging a Mixed Python and C Language Stack
Debugging is difficult. Debugging across multiple languages is especially challenging, and debugging across devices often requires a team with varying skill...
18 MIN READ
Jun 23, 2022
Just Released: CUTLASS v2.9
The latest version of CUTLASS offers users BLAS3 operators accelerated by tensor cores, Python integrations, GEMM compatibility extensions, and more.
1 MIN READ

Mar 23, 2022
Boosting Application Performance with GPU Memory Prefetching
NVIDIA GPUs have enormous compute power and typically must be fed data at high speed to deploy that power. That is possible, in principle, because GPUs also...
10 MIN READ

Feb 10, 2022
Implementing High-Precision Decimal Arithmetic with CUDA int128
“Truth is much too complicated to allow anything but approximations.” -- John von Neumann The history of computing has demonstrated that there is no limit...
19 MIN READ
Dec 08, 2020
Fast, Flexible Allocation for NVIDIA CUDA with RAPIDS Memory Manager
When I joined the RAPIDS team in 2018, NVIDIA CUDA device memory allocation was a performance problem. RAPIDS cuDF allocates and deallocates memory at high...
24 MIN READ
Jun 19, 2017
Unified Memory for CUDA Beginners
My previous introductory post, "An Even Easier Introduction to CUDA C++", introduced the basics of CUDA programming by showing how to write a simple program...
16 MIN READ
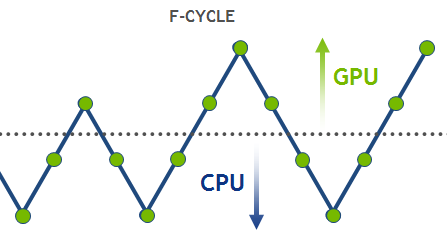
Feb 23, 2016
High-Performance Geometric Multi-Grid with GPU Acceleration
Linear solvers are probably the most common tool in scientific computing applications. There are two basic classes of methods that can be used to solve an...
16 MIN READ

Oct 19, 2015
Cutting Edge Parallel Algorithms Research with CUDA
Leyuan Wang, a Ph.D. student in the UC Davis Department of Computer Science, presented one of only two “Distinguished Papers” of the 51 accepted at Euro-Par...
14 MIN READ
Oct 12, 2015
Accelerating Materials Discovery with CUDA
In this post, we discuss how CUDA has facilitated materials research in the Department of Chemical and Biomolecular Engineering at UC Berkeley and Lawrence...
15 MIN READ

Aug 06, 2015
Voting and Shuffling to Optimize Atomic Operations
2iSome years ago I started work on my first CUDA implementation of the Multiparticle Collision Dynamics (MPC) algorithm, a particle-in-cell code used to...
10 MIN READ
Feb 18, 2015
BIDMach: Machine Learning at the Limit with GPUs
Deep learning has made enormous leaps forward thanks to GPU hardware. But much Big Data analysis is still done with classical methods on sparse data. Tasks like...
15 MIN READ

Sep 02, 2014
3 Versatile OpenACC Interoperability Techniques
OpenACC is a high-level programming model for accelerating applications with GPUs and other devices using compiler directives compiler directives to specify...
8 MIN READ