Fortran

Jun 12, 2022
Using Fortran Standard Parallel Programming for GPU Acceleration
Standard languages have begun adding features that compilers can use for accelerated GPU and CPU parallel programming, for instance, do concurrent loops and...
12 MIN READ
Nov 18, 2020
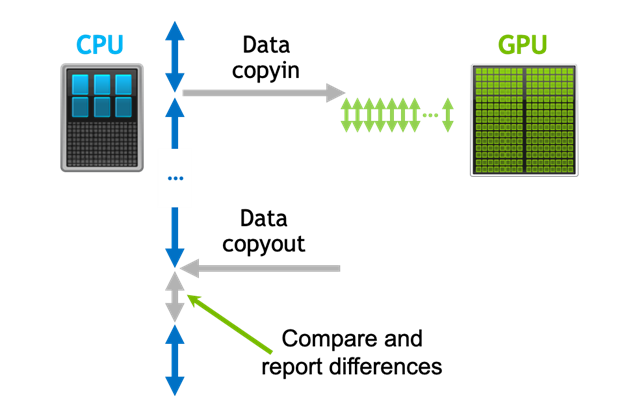
Detecting Divergence Using PCAST to Compare GPU to CPU Results
Parallel Compiler Assisted Software Testing (PCAST) is a feature available in the NVIDIA HPC Fortran, C++, and C compilers. PCAST has two use cases. The first...
14 MIN READ

Nov 16, 2020
Accelerating Fortran DO CONCURRENT with GPUs and the NVIDIA HPC SDK
Fortran developers have long been able to accelerate their programs using CUDA Fortran or OpenACC. For more up-to-date information, please read Using Fortran...
13 MIN READ
Aug 07, 2020
Bringing Tensor Cores to Standard Fortran
Tuned math libraries are an easy and dependable way to extract the ultimate performance from your HPC system. However, for long-lived applications or those that...
10 MIN READ
Apr 02, 2019
Tensor Core Programming Using CUDA Fortran
The CUDA Fortran compiler from PGI now supports programming Tensor Cores with NVIDIA’s Volta V100 and Turing GPUs. This enables scientific programmers using...
12 MIN READ

Jul 16, 2018
Using OpenACC to Port Solar Storm Modeling Code to GPUs
Solar storms consist of massive explosions on the Sun that can release the energy of over 2 billion megatons of TNT in the form of solar flares and Coronal Mass...
39 MIN READ

Jul 19, 2016
GPU-Accelerated PC Solves Complex Problems Hundreds of Times Faster Than Massive CPU-only Supercomputers
Russian scientists from Lomonosov Moscow State University used an ordinary GPU-accelerated desktop computer to solve complex quantum mechanics equations in just...
2 MIN READ

Oct 29, 2015
Performance Portability for GPUs and CPUs with OpenACC
New PGI compiler release includes support for C++ and Fortran applications to run in parallel on multi-core CPUs or GPU accelerators. OpenACC gives scientists...
1 MIN READ

Jul 13, 2015
Introducing the NVIDIA OpenACC Toolkit
Programmability is crucial to accelerated computing, and NVIDIA's CUDA Toolkit has been critical to the success of GPU computing. Over three million CUDA...
4 MIN READ

Mar 08, 2015
12 GTC 2015 Sessions Not to Miss
With one week to go until we all descend on GTC 2015, I've scoured through the list of Accelerated Computing sessions and put together 12 diverse "not to miss"...
7 MIN READ
Oct 31, 2012
Do More, Code Less with ArrayFire GPU Matrix Library
This is a guest post by Chris McClanahan from ArrayFire (formerly AccelerEyes). ArrayFire is a fast and easy-to-use GPU matrix library developed by ArrayFire....
8 MIN READ
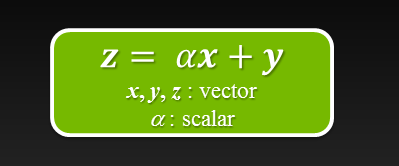
Jul 02, 2012
Six Ways to SAXPY
For even more ways to SAXPY using the latest NVIDIA HPC SDK with standard language parallelism, see N Ways to SAXPY: Demonstrating the Breadth of GPU...
8 MIN READ

Mar 25, 2012
An OpenACC Example (Part 2)
You may want to read the more recent post Getting Started with OpenACC by Jeff Larkin. In my previous post I added 3 lines of OpenACC directives to a...
8 MIN READ

Mar 19, 2012
An OpenACC Example (Part 1)
You may want to read the more recent post Getting Started with OpenACC by Jeff Larkin. In this post I'll continue where I left off in my introductory...
11 MIN READ

Mar 12, 2012
OpenACC: Directives for GPUs
NVIDIA has made a lot of progress with CUDA over the past five years; we estimate that there are over 150,000 CUDA developers, and important science is...
5 MIN READ