OpenACC
Jan 18, 2024
Webinar: Quantum ESPRESSO on GPUs: Porting Strategy and Results
Explore the status of Quantum ESPRESSO porting strategies that enable state-of-the-art performance on HPC systems.
1 MIN READ

Dec 01, 2023
Webinar: Analysis of OpenACC Validation and Verification Testsuite
On December 7, learn how to verify OpenACC implementations across compilers and system architectures with the validation testsuite.
1 MIN READ

Oct 05, 2023
Just Released: NVIDIA HPC SDK 23.9
This NVIDIA HPC SDK 23.9 update expands platform support and provides minor updates.
1 MIN READ

Jul 31, 2023
Just Released: NVIDIA HPC SDK v23.7
NVIDIA HPC SDK version 23.7 is now available and provides minor updates and enhancements.
1 MIN READ

May 25, 2023
Just Released: NVIDIA HPC SDK v23.5
This update expands platform support and provides minor updates.
1 MIN READ
May 17, 2023
Webinar: Performant Multiphase Flow Simulation at Leadership-Class Scale
On June 6, learn how researchers use OpenACC for GPU acceleration of multiphase and compressible flow solvers that obtain speedups at scale.
1 MIN READ

Apr 28, 2023
Microsoft and TempoQuest Accelerate Wind Energy Forecasts with AceCast
Accurate weather modeling is essential for companies to properly forecast renewable energy production and plan for natural disasters. Ineffective and...
7 MIN READ

Apr 03, 2023
Just Released: NVIDIA HPC SDK v23.3
Version 23.3 expands platform support and provides minor updates to the NVIDIA HPC SDK.
1 MIN READ

Jan 25, 2023
Just Released: NVIDIA HPC SDK v23.1
Version 23.1 of the NVIDIA HPC SDK introduces CUDA 12 support, fixes, and minor enhancements.
1 MIN READ

Nov 17, 2022
New Asynchronous Programming Model Library Now Available with NVIDIA HPC SDK v22.11
Celebrating the SuperComputing 2022 international conference, NVIDIA announces the release of HPC Software Development Kit (SDK) v22.11. Members of the NVIDIA...
4 MIN READ

Jul 13, 2022
Upcoming Event: OpenACC and Hackathons Summit 2022
Join this digital conference from August 2-4 to learn how science is being advanced through the work done at Open Hackathons or accelerated using OpenACC.
1 MIN READ

Jun 12, 2022
Using Fortran Standard Parallel Programming for GPU Acceleration
Standard languages have begun adding features that compilers can use for accelerated GPU and CPU parallel programming, for instance, do concurrent loops and...
12 MIN READ

Feb 24, 2022
From Earth Sciences to Factory Production: GPU Hackathon Optimizes Modeling Results
While the world is continuously changing, one constant is the ongoing drive of developers to tackle challenges using innovative technologies. The recent Taiwan...
5 MIN READ
Nov 18, 2020
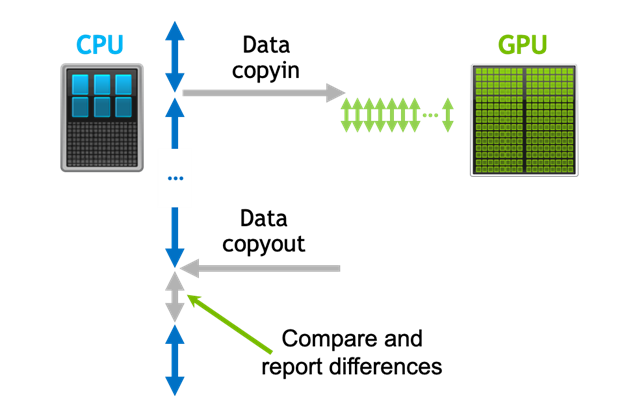
Detecting Divergence Using PCAST to Compare GPU to CPU Results
Parallel Compiler Assisted Software Testing (PCAST) is a feature available in the NVIDIA HPC Fortran, C++, and C compilers. PCAST has two use cases. The first...
14 MIN READ

Jul 24, 2020
OpenACC Summit 2020 Goes Digital
This year’s OpenACC 2020 Summit is going digital. Scheduled from August 31st to September 4th, the OpenACC Summit brings together users of the OpenACC...
1 MIN READ
Jun 23, 2020
Government of India, NVIDIA, and OpenACC Hackathon Helps Develop COVID-19 Solutions
The Government of India’s Center for Development of Advanced Computing (C-DAC) under Ministry of Electronics and IT (MeitY) in association with NVIDIA, and...
2 MIN READ