Six scientific computing teams from around the world spent an intense week late last year porting their applications to GPUs using OpenACC directives. The Oak Ridge Leadership Computing Facility (OLCF) hosted its first ever OpenACC Hackathon in Knoxville, Tennessee. Paired with two GPU mentors, each team of scientific developers set forth on the journey to accelerate their code with GPUs.
Dr. Misun Min, a computational scientist at Argonne National Laboratory, led the NekCEM Team and she shared the results of accelerating NekCEM with OpenACC and NVIDIA GPUDirect™ communication.
Who were the NekCEM hackathon team members, and how much GPU computing experience did your team have?
I have only six months experience; but at the time of the Hackathon, I didn’t really have any. The other members included Matthew Otten from Cornell University (six months GPU computing experience), Jing Gong from KTH in Sweden (two years of OpenACC experience), and Azamat Mametjanov from Argonne. The team also had close interactions with Nek5000 developer Paul Fischer at UIUC for useful discussions.
Who were your mentors?
Two mentors from Cray Inc.: Aaron Vose and John Levesque. Aaron and John provided strong technical support to boost the performance of a GPU-enabled NekCEM version.
First, what is NekCEM?
NekCEM (Nekton for Computational ElectroMagnetics) is an open-source code designed for predictive modeling of electromagnetic systems, such as linear accelerators, semiconductors, plasmonic devices, and quantum systems described by the Maxwell, Helmholtz, drift-diffusion, and Schrödinger or density matrix equations. The code is based on high-order discretizations of the underlying partial differential equations using spectral element (SE) and spectral-element discontinuous Galerkin (SEDG) schemes that have been shown to require order-of-magnitude fewer grid points than do conventional low-order schemes for the same accuracy. NekCEM uses globally unstructured meshes comprising body-fitted curvilinear hexahedral elements, which allow the discrete operators to be expressed as matrix-matrix products applied to arrays of the tensor product basis of Lagrange interpolation polynomials on the Gauss-Lobatto-Legendre quadrature points. The tight coupling of the degrees of freedom within elements leads to efficient data reuse while requiring boundary-minimal (unit-depth-stencil) data communication to effect flux exchanges between neighboring elements.
What were your team’s goals going into the OpenACC Hackathon?
The team had two goals: (1) to develop a high-performance GPU-based operational variant of NekCEM that supports the full functionality of the existing CPU-only code in Fortran/C and (2) to perform analysis to find performance bottlenecks and infer potential scalability for GPU-based architectures of the future.
Why did you choose OpenACC?
OpenACC was chosen as a strategy for porting NekCEM to multiple GPUs because of the relative ease of the pragma-based programming model. During the Hackathon, significant efforts included the development of an OpenACC implementation of the local gradient (see Listing 1) and spectral element curl operator (see Listing 2) for solving the Maxwell equations and a tuned GPUDirect gather-scatter kernel for nearest-neighbor flux exchanges (see Listing 3).
!$ACC DATA PRESENT(u1r,u1s,u1t,u2r,u2s,u2t,u3r,u3s,u3t)
!$ACC& PRESENT(u1,u2,u3,d,dtrans)
p1=dclock()-p0
ptime=ptime+p1
!$ACC PARALLEL LOOP COLLAPSE(4) GANG WORKER VECTOR
!$ACC& private(tmpr1,tmpr2,tmpr3,tmps1,tmps2,tmps3,
!$ACC& tmpt1,tmpt2,tmpt3)
!dir$ NOBLOCKING
do e = 1,nelt
do k = 1,nz1
do j = 1,ny1
do i = 1,nx1
tmpr1 = 0.0
tmpr2 = 0.0
tmpr3 = 0.0
tmps1 = 0.0
tmps2 = 0.0
tmps3 = 0.0
tmpt1 = 0.0
tmpt2 = 0.0
tmpt3 = 0.0
!$ACC LOOP SEQ
do l=1,nx1
tmpr1=tmpr1+d(i,l)*u1(l,j,k,e)
tmpr2=tmpr2+d(i,l)*u2(l,j,k,e)
tmpr3=tmpr3+d(i,l)*u3(l,j,k,e)
tmps1=tmps1+d(j,l)*u1(i,l,k,e)
tmps2=tmps2+d(j,l)*u2(i,l,k,e)
tmps3=tmps3+d(j,l)*u3(i,l,k,e)
tmpt1=tmpt1+d(k,l)*u1(i,j,l,e)
tmpt2=tmpt2+d(k,l)*u2(i,j,l,e)
tmpt3=tmpt3+d(k,l)*u3(i,j,l,e)
enddo
u1r(i,j,k,e) = tmpr1
u2r(i,j,k,e) = tmpr2
u3r(i,j,k,e) = tmpr3
u1s(i,j,k,e) = tmps1
u2s(i,j,k,e) = tmps2
u3s(i,j,k,e) = tmps3
u1t(i,j,k,e) = tmpt1
u2t(i,j,k,e) = tmpt2
u3t(i,j,k,e) = tmpt3
enddo
enddo
enddo
enddo
!$ACC END PARALLEL LOOP
!$ACC END DATA
!$ACC DATA PRESENT(u1r,u1s,u1t,u2r,u2s,u2t,u3r,u3s,u3t,w1,w2,w3)
!$ACC& PRESENT(w3mn,rxmn,sxmn,txmn,rymn,symn,tymn,rzmn,szmn,tzmn)
p1=dclock()-p0
ptime=ptime+p1
!$ACC PARALLEL LOOP COLLAPSE(4) GANG WORKER VECTOR
do e = 1,nelt
do k = 1,nz1
do j = 1,ny1
do i = 1,nx1
w1(i,j,k,e)= (u3r(i,j,k,e)*rymn(i,j,k,e)
$ + u3s(i,j,k,e)*symn(i,j,k,e)
$ + u3t(i,j,k,e)*tymn(i,j,k,e)
$ - u2r(i,j,k,e)*rzmn(i,j,k,e)
$ - u2s(i,j,k,e)*szmn(i,j,k,e)
$ - u2t(i,j,k,e)*tzmn(i,j,k,e))*w3mn(i,j,k)
w2(i,j,k,e)= (u1r(i,j,k,e)*rzmn(i,j,k,e)
$ + u1s(i,j,k,e)*szmn(i,j,k,e)
$ + u1t(i,j,k,e)*tzmn(i,j,k,e)
$ - u3r(i,j,k,e)*rxmn(i,j,k,e)
$ - u3s(i,j,k,e)*sxmn(i,j,k,e)
$ - u3t(i,j,k,e)*txmn(i,j,k,e))*w3mn(i,j,k)
w3(i,j,k,e)= (u2r(i,j,k,e)*rxmn(i,j,k,e)
$ + u2s(i,j,k,e)*sxmn(i,j,k,e)
$ + u2t(i,j,k,e)*txmn(i,j,k,e)
$ - u1r(i,j,k,e)*rymn(i,j,k,e)
$ - u1s(i,j,k,e)*symn(i,j,k,e)
$ - u1t(i,j,k,e)*tymn(i,j,k,e))*w3mn(i,j,k)
enddo
enddo
enddo
enddo
!$ACC END PARALLEL LOOP
!$ACC END DATA
//* (1) local gather *//
for(k=0;k<vn;++k) {="" #<span="" class="hiddenSpellError" pre="" data-mce-bogus="1">pragma acc parallel loop gang vector present(u[0:uds],map[0:m_size],mapf[0:m_nt*2]) private(i,j,t) async(k+1)
for(i=0;i
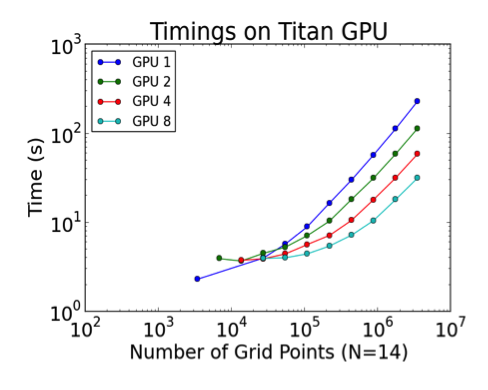
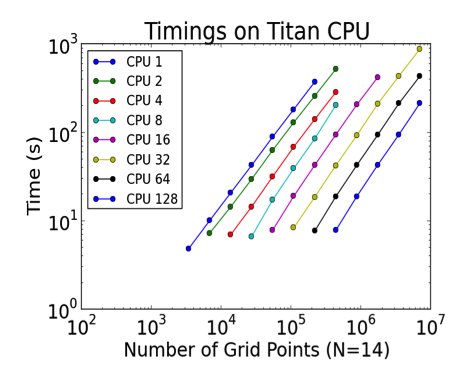
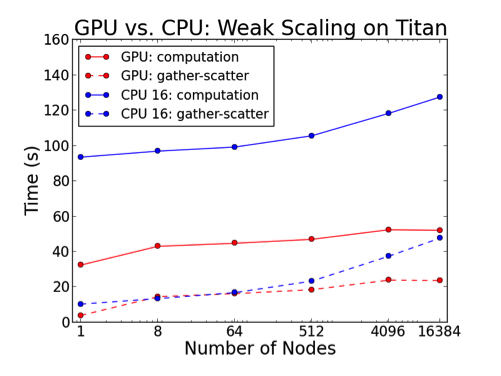
We examined scaling limits for both GPU and CPU runs as a function of problem size (measured in number of grid points, n). The column and the row of the dots in Figures 1 and 2 correspond to strong and weak scaling, respectively, demonstrating that the lower-bound for effective GPU-based solution of Maxwell’s equations with SEDG formulation is approximately n=105. We also explored multi-GPU scalability limits on up to 16,384 GPUs on the Titan Cray XK7, the nation’s most powerful supercomputer for open science.
What results did you achieve with OpenACC?
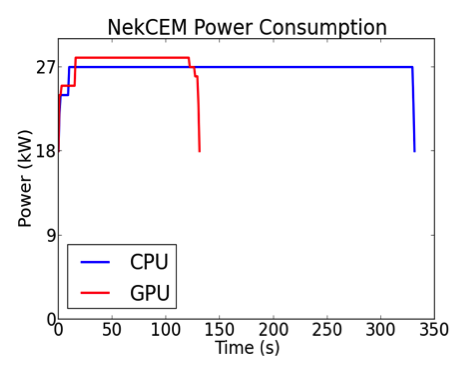
The effort resulted in a twofold speedup over a highly tuned CPU-only version of the code on the same number of nodes (262,144 MPI ranks) for problem sizes of up to 6.9 billion grid points (see Figure 3). Run-time power consumption data for isolated two-cabinet jobs (192 nodes) demonstrated that the GPU runs required only 39% of the energy needed for comparable CPU runs (see Figure 4).
Learn More
Want to learn more? Check out these related sessions from GTC 2015.
- Misun and a few of the other OpenACC Hackathon teams shared their experience – the recording is now live.
- Aaron Vose, benchmark and application analyst at Cray Inc. and the NekCEM mentor presented a talk about the “lessons learned” from porting the computational physics applications to the Titan supercomputer with hybrid OpenACC and OpenMP.
- Featured Panel: GPU Computing with OpenACC and OpenMP discusses the current state of GPU programming using compiler directives.
OLCF has partnered with NCSA and CSCS to host three GPU Hackathons this year. They stress that you do not need to have prior GPU experience; you can visit the OLCF website for more information. It’s a priceless opportunity to work with OpenACC experts and to get your code running on GPUs.