In this post we introduce the “register cache”, an optimization technique that develops a virtual caching layer for threads in a single warp. It is a software abstraction implemented on top of the NVIDIA GPU shuffle primitive. This abstraction helps optimize kernels that use shared memory to cache thread inputs. When the kernel is transformed by applying this optimization, the data ends up being distributed across registers in the threads of each warp, and shared memory accesses are replaced with accesses to registers in other threads by using shuffle, thereby enabling significant performance benefits.
We develop the register cache abstraction and show how to use it in the context of a simple kernel that computes a 1D-stencil. We then provide a general recipe for transforming a kernel to use the register cache, evaluate its performance, and discuss its limitations. A more elaborate analysis and evaluation are presented in our paper: “Fast Multiplication in Binary Fields on GPUs via Register Cache.”
Where is the Warp-Level Cache?
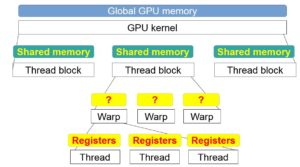
GPU kernels may store data in the following three memory layers: global memory, shared memory and registers (see Figure 1). These layers effectively form a hierarchy in terms of size, performance and scope of sharing: the largest and slowest—global memory—is shared across all the kernel threads; smaller but much faster shared memory is shared across the threads of a single thread block; and the smallest and fastest—registers—are private to each thread.
You can view each layer in the memory hierarchy as a cache for the respective layer in the execution hierarchy. Specifically, shared memory serves as a cache for the threads in a thread block, while registers allow “caching” of data in a single thread.
Interestingly, as Figure 1 shows, a single warp does not have its own explicit caching layer. Thus, kernels that follow a warp-centric design do not have a specialized memory layer in hardware in which to cache the warp’s input.
Caching in Registers Using Shuffle
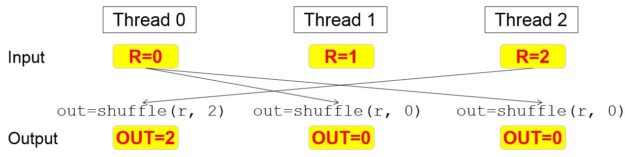
In the CUDA Kepler microarchitecture (2012) NVIDIA introduced the SHFL (shuffle) instruction, which enables intra-warp communication. The primitive function shfl_sync(m, r, t) enables an issuing thread to share a value stored in register r while reading the value shared by thread t in the same warp (m is a 32-bit mask of participating threads within the warp). Figure 2 presents the semantics of shfl_sync(). More detailed description can be found in a previous Parallel Forall blog post.
There are a few good reasons to use registers for data sharing among threads in a warp.
- The bandwidth to registers is higher and the access latency is lower compared to shared memory.
- The use of
shfl_sync()eliminates the need for expensive thread block-wise synchronization via__syncthreads()or a memory fence between writing and reading threads (as long as there is no intra-warp divergence), which is otherwise necessary for sharing data via shared memory. - In modern GPUs the shared memory size is only 64KB, while the register file size is 256KB. Consequently, if there are unused registers they can be used to augment shared memory.
Unfortunately, the use of shuffle is fairly complex. In particular, if a kernel has already been written to use shared memory, modifying it to use shuffle may require significant algorithmic changes.
The technique presented here aims to help optimize kernels by replacing shared memory accesses with shuffles. It targets a specific yet quite common case: when shared memory is used to cache the kernel input.
To guide the transformation we redesign the code to use a “virtual” warp-level cache we call a register cache. Each thread holds and manages a local partition of the cache in an array rc stored in its registers. The cache management is logically decoupled from the rest of the program, which simplifies the development.
There is no implementation of a real cache, of course (no replacement policy, etc.). However, we found that building a mental picture of such a cache while optimizing the code greatly simplifies the process.
We now explain the idea by developing a simple example 1D stencil kernel.
Register Cache by Example: 1D Stencil
Definition. 1D k-stencil: Given an array A of size n, the k-stencil of A is an array B of size n-2k where B[i] = (A[i]+…+A[i+2k])/(2k+1). For example, array B is the 1-stencil of array A.
| A: | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| B: | 1 | 2 | 3 | 4 | 5 | 6 |
B[0] = (A[0] + A[1] + A[2])/3 = (0 + 1 + 2)/3 = 1
B[1] = (A[1] + A[2] + A[3])/3 = (1 + 2 + 3)/3 = 2
…
B[5] = (A[5] + A[6] + A[7])/3 = (5 + 6 + 7)/3 = 6
To compute a 1D k-stencil each input element (except for margins) is read 2k+1 times. Thus, any implementation must cache the input in order to exploit data reuse. For simplicity we drop 1D from the notation and use k=1.
We start with a simple implementation of the kernel which uses shared memory, and then show how we transform it to use shuffle with the help of the register cache abstraction.
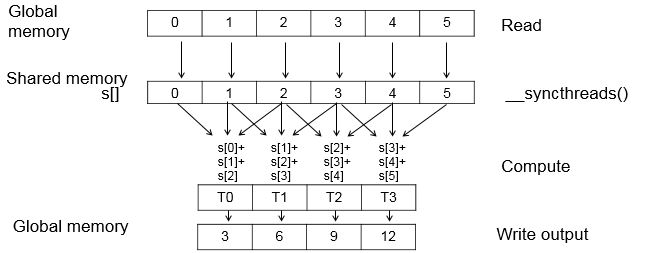
Step 1: Shared Memory Implementation
We start with the following implementation (see Listing 1)
- Copy input from global memory into a temporary array in shared memory using all threads in each block.
- Wait until the input is stored in shared memory by calling
__syncthreads. - Compute one output element.
- Store the results in global memory.
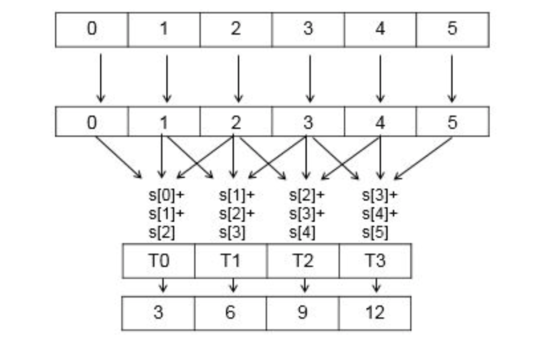
Figure 3 illustrates the computation steps.
__global__ void one_stencil (int *A, int *B, int sizeOfA)
{
extern __shared__ int s[];
// Id of thread in the block.
int localId = threadIdx.x;
// The first index of output element computed by this block.
int startOfBlock = blockIdx.x * blockDim.x;
// The Id of the thread in the scope of the grid.
int globalId = localId + startOfBlock;
if (globalId >= sizeOfA)
return;
// Fetching into shared memory.
s[localId] = A[globalId];
if (localId < 2 && blockDim.x + globalId < sizeOfA) {
s[blockDim.x + localId] = A[blockDim.x + globalId];
}
// We must sync before reading from shared memory.
__syncthreads();
// Each thread computes a single output.
if (globalId < sizeOfA - 2)
B[globalId] = (s[localId] + s[localId + 1] + s[localId + 2]) / 3;
}
Step 2: Identify Warp Inputs
Given that i is the index of the output element computed by thread 0 in a warp, the warp calculates the output elements i, i+1, …, i+31, and depends on 34 input elements i-1, …, i+32 denoted as input array.
Step 3: Determine Input Distribution Among the Threads
We distribute the input among the registers of each thread in a warp. In our example here we use a round-robin distribution of input arrays among the threads. In this scheme, input[i] is assigned to thread j such that j = i % 32. Thread 0 and thread 1 store two elements each, while all the other threads store only one array element. We denote the first cached element in each thread’s local partition as rc[0] and the second as rc[1]. Observe that this distribution scheme mimics the data distribution across the banks of shared memory.
Table 1 illustrates the distribution of inputs among the threads assuming 4 threads in a warp.
| Thread | T0 | T1 | T2 | T3 | ||||
|---|---|---|---|---|---|---|---|---|
| rc | input[0] |
input[4] |
input[1] |
input[5] |
input[2] |
input[3] |
||
Step 4: Communication and Computation
We split the kernel into communication and computation phase(s). In the communication phase threads effectively access the register cache. In the computation phase each thread, locally, performs some arithmetic or logical operation using the values it read from the cache.
Here comes the main technical component of the register cache recipe. We introduce two communication primitives used by the threads in the warp, to make it easier to design the communication phase:
Read(src_tid, remote_reg): Read data stored in threadsrc_tidin remote variableremote_reg.Publish(local_reg): Publish local data stored in variablelocal_reg.
Each communication phase is composed of one or more of these primitives. Note that for one thread to Read, another thread has to Publish the requested data stored in its local registers.
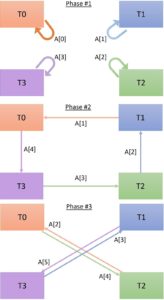
We identify three communication phases in 1-stencil: one for each input element read by each thread. Table 2 lists all Read (R) and Publish (P) operations performed by each thread, assuming 4 threads in a warp, and Figure 4 illustrates the communication phases.
Read(j, i) indicates a read from thread j of its element rc[i]. The first communication phase is local, and provided for clarity.
| T0 | T1 | T2 | T3 | Explanation |
|---|---|---|---|---|
| v=R(T0, rc[0])
P(rc[0]) |
v=R(T1, rc[0])
P(rc[0]) |
v=R(T2, rc[0])
P(rc[0]) |
v=R(T3, rc[0])
P(rc[0]) |
Communication phase: Each thread reads the first input element it needs. For example, T0 reads rc[0] from T0 which contains input[0]. Notice that each thread publishes the value it receives. |
| _ac += v
(=input[0]) |
_ac += v
(=input[0]) |
_ac += v
(=input[0]) |
_ac += v
(=input[0]) |
Computation phase: Each thread adds the value it has just read to its local accumulator. |
| v=R(T1, rc[0])
P(rc[1]) |
v=R(T2, rc[0])
P(rc[0]) |
v=R(T3, rc[0])
P(rc[0]) |
v=R(T0, rc[1])
P(rc[0]) |
Communication phase: Each thread reads the next value. Notice that T3 now reads input[4] which is stored in rc[1] of T0, therefore thread T0 publishes rc[1].
For example, this phase T0 reads input[1] from rc[0] from T1. |
| _ac += v
(=input[0]+ input[1]) |
_ac += v
(=input[1]+ input[2]) |
_ac += v
(=input[2]+ input[3]) |
_ac += v
(=input[3]+ input[4]) |
Computation phase: Each thread adds the value it has just read to its local accumulator. |
| v=R(T2, rc[0])
P(rc[1]) |
v=R(T3, rc[0])
P(rc[1]) |
v=R(T0, rc[1])
P(rc[0]) |
v=R(T1, rc[1])
P(rc[0]) |
Communication phase: Each thread reads the last value it needs. |
| _ac += v | _ac += v | _ac += v | _ac += v | Computation phase: Each thread adds the value is has just read to its local accumulator.. |
After the computations described in Table 2 are finished each thread holds the value _ac that stores the output it next writes to global memory.
Step four: Replace Publish-Reads with shfl_sync()
CUDA doesn’t provide the Read and Publish primitives, but we can merge them using the shuffle primitive to implement the code in a real GPU. Say thread t_i calls Read(t_j, rc[0]) and Publish(r_i). We can implement these two calls using shfl_sync(t_j, r_i). All that remains is to efficiently compute thread and register indexes in the shfl_sync() calls while avoiding divergence.
This step concludes the transformation, and now the implementation does not use shared memory.
There is a problem in the case where two threads call Read(t_i, v) and Read(t_i, u), where v and u are two different values stored by t_i. One of the threads will not receive the value since t_i can publish only a single value in each cache access. Two or more accesses are therefore needed to satisfy these requests. We call this case a register cache conflict.
With this translation from Publish + Read into shfl_sync we can implement the full 1-stencil without using shared memory (Listing 2) . The full implementation is available in this repository.
__global__ void one_stencil_with_rc (int *A, int *B, int sizeOfA)
{
// Declaring local register cache.
int rc[2];
// Id of thread in the warp.
int localId = threadIdx.x % WARP_SIZE;
// The first index of output element computed by this warp.
int startOfWarp = blockIdx.x * blockDim.x + WARP_SIZE*(threadIdx.x / WARP_SIZE);
// The Id of the thread in the scope of the grid.
int globalId = localId + startOfWarp;
if (globalId >= sizeOfA)
return;
// Fetching into shared memory.
rc[0] = A[globalId];
if (localId < 2 & & WARP_SIZE + globalId < sizeOfA)
{
rc[1] = A[WARP_SIZE + globalId];
}
// Each thread computes a single output.
int ac = 0;
int toShare = rc[0];
for (int i = 0 ; i < 3 ; ++i)
{
// Threads decide what value will be published in the following access.
if (localId < i)
toShare = rc[1];
// Accessing register cache.
unsigned mask = __activemask();
ac += __shfl_sync(mask, toShare, (localId + i) % WARP_SIZE);
}
if (globalId < sizeOfA - 2)
B[globalId] = ac/3;
}
Evaluation
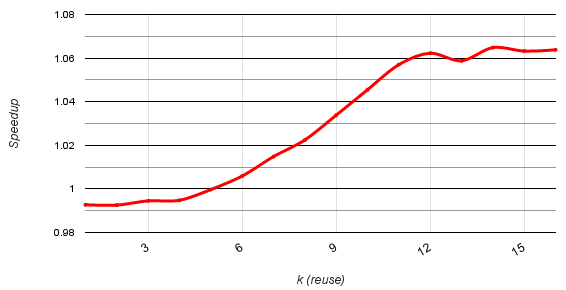
Figure 5 shows the speedup of the register cache over shared memory implementation of a k-stencil for increasing values of k. We used a GTX-1080 GPU and CUDA 9 to run the experiments.
For small values of k the data reuse is small or negligible, hence the speedup is small, but as k grows, the reuse achieved by register cache increases and the speedup as well.
Thread coarsening
The speedup reaches a plateau starting at k=12, since the register cache also performs more global memory accesses due to the overlapping edges of the input, which are read twice by two consecutive warps.
One common technique to reduce these global memory accesses is thread coarsening. This technique increases the number of outputs produced by each thread, and thus enables some of the input data to be reused across iterations by storing it in registers.
In the case of the register cache, thread coarsening becomes critical to achieve the desired performance improvements. The reason lies in the small number of threads sharing the cache. Since the register cache is limited to the threads of a single warp, only the inputs necessary for the warp threads are prefetched and cached. However, the input reuse might occur across consecutive warps. For the 1-stencil kernel we develop here, the input to the first thread in warp i is the same as the input to the last thread in warp i-1. Hence, this value is read twice from the global memory. For 32 warps per thread block, a register cache implementation performs 34 * 32 = 1088 global memory accesses, which is 6% more than the number of global memory accesses in a standard implementation using shared memory. Note that as k grows, the number of redundant global memory accesses becomes high. For example, almost half of the accesses are redundant for k= 16.
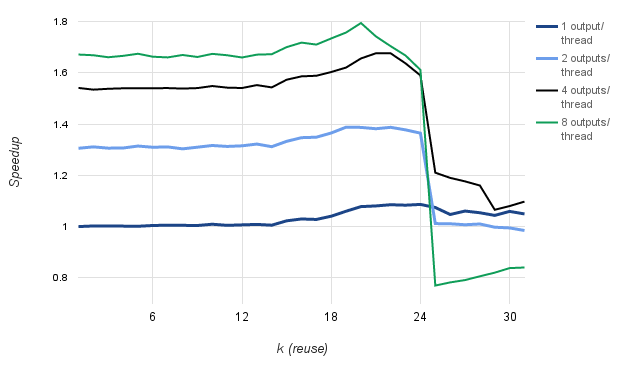
Thread coarsening helps reduce the effect of redundant global memory accesses. Figure 6 shows the speedup over a shared memory implementation achieved by computing with a varying number of outputs per thread (1 to 8), for different values of k. Thanks to thread coarsening, the register cache version achieves the speedup of up to 1.8x. For larger values of k the number of registers required for the cache is too large to fit in the physical registers and the compiler spills them to local memory (usually in L1 cache, but also global memory if not enough space), so the performance drops.
When Should You Use Register Caching?
There are cases where the register cache is not applicable. First, the access pattern should be known at compile time. Second, the efficiency of the register cache is predicated on the availability of spare registers. Otherwise, registers start spilling to global memory, leading to a dramatic performance drop, as is the case for k=25 in Figure 6.
CUDA 9 and Cooperative Groups
CUDA 9, introduced by NVIDIA at GTC 2017 includes Cooperative Groups, a new programming model for organizing groups of communicating and cooperating parallel threads. In particular, programmers should not rely on implicit synchronization of threads within a warp. Cooperative Groups makes it easier to explicitly synchronize groups of threads—especially at the warp level. Additionally, existing primitives such as __shfl(), which assumed implicit full-warp synchronization, have been deprecated. The new synchronizing versions allow the programmer to explicitly synchronize a subset of threads in a warp.
In more detail, starting with CUDA 9, the __shfl() function (along with related variants, such as __shfl_down()) is deprecated, and you should use the __shfl_sync() function instead, as we have done in all code in this post.
For example in our code, we replaced the call
__shfl(v, i)
with
unsigned mask = __activemask(); __shfl_sync(mask, v, i);
Here __activemask() returns a mask of all currently active (in other words, not blocked by execution flow) threads. In cases where the required mask is known (the common case is all threads in the warp), that can be specified explicitly instead of using __activemask().
You can also use Cooperative Groups to create a statically sized tiled partition of the thread block group. Statically sized groups support the shfl() method (which calls shfl_sync() internally, passing a mask that includes all threads in the group). Here’s how to create a warp-sized group that supports shfl().
namespace cg = cooperative_groups; ... auto tile = cg::tiled_partition<32>(cg::this_thread_block()); tile.shfl(v, i);
In pre-Volta GPUs each warp maintained a single program counter (PC), pointing to the next instruction executed by the warp as well as a mask of all the currently active threads in the warp. Independent thread scheduling in Volta GPUs maintains a PC for every thread, enabling separate and independent execution flows of threads in a single warp, which gives more freedom to the GPU scheduler.
Changing all __shfl() calls in our code to __shfl_sync() did not affect the execution of our code on Pascal GPUs (NVIDIA GeForce GTX 1080), and this change will make the code safe to execute on Volta GPUs and beyond.
Additional Details
For additional details regarding the implementation and internals of the register cache, and its use for the computation of finite field multiplication, we refer the readers to the paper by Hamilis, Ben-Sasson,Tromer and Silberstein. The source code for the examples in this post is available on Github.