Double-precision floating point (FP64) has been the de facto standard for doing scientific simulation for several decades. Most numerical methods used in engineering and scientific applications require the extra precision to compute correct answers or even reach an answer. However, FP64 also requires more computing resources and runtime to deliver the increased precision levels.
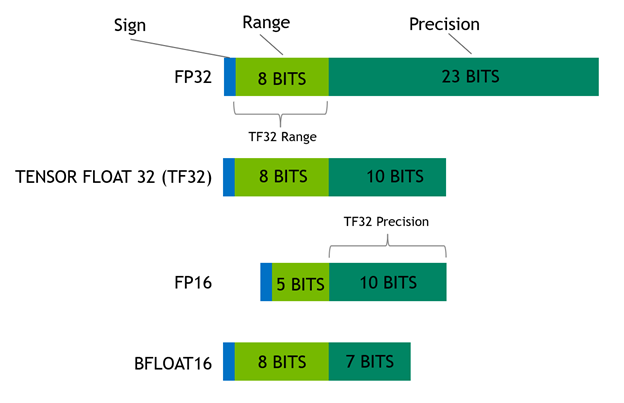
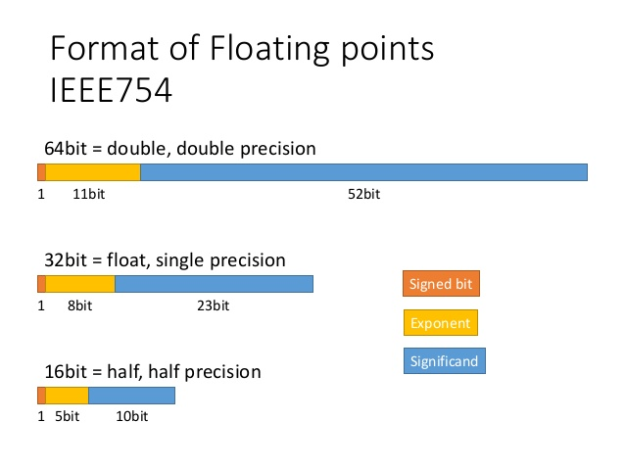
Problem complexity and the sheer magnitude of data coming from various instruments and sensors motivate researchers to mix and match various approaches to optimize compute resources, including different levels of floating-point precision. Researchers have experimented with single-precision (FP32) in the fields of life science and seismic for several years. In recent years, the big bang for machine learning and deep learning has focused significant attention on half-precision (FP16). Using reduced precision levels can accelerate data transfers rates,increase application performance, and reduce power consumption, especially on GPUs with Tensor Core support for mixed-precision. Figure 1 describes the IEEE 754 standard floating point formats for FP64, FP32, and FP16 precision levels.
Using Tensor Cores for Mixed-Precision
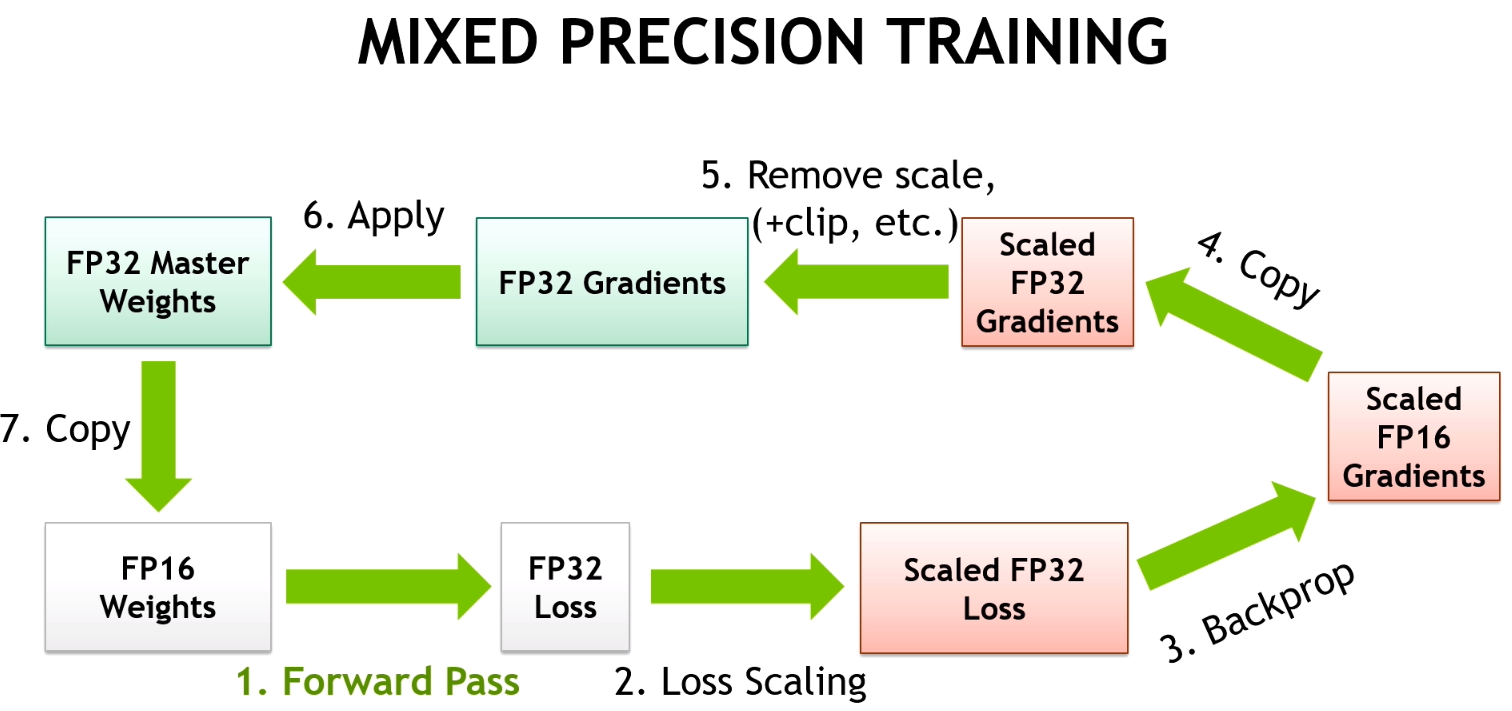
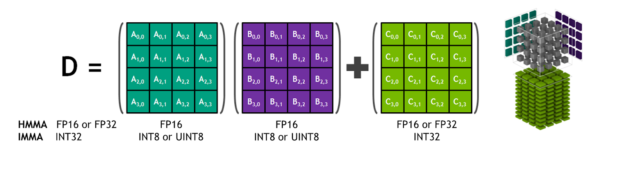
NVIDIA Tesla V100 includes both CUDA Cores and Tensor Cores, allowing computational scientists to dramatically accelerate their applications by using mixed-precision. Using FP16 with Tensor Cores in V100 is just part of the picture. Accumulation to FP32 sets the Tesla V100 and Turing chip architectures apart from all the other architectures that simply support lower precision levels. Volta V100 and Turing architectures, enable fast FP16 matrix math with FP32 compute, as figure 2 shows. Tensor Cores provide up to 125 TFlops FP16 performance in the Tesla V100. The 16x multiple versus FP64 within the same power budget has prompted researchers to explore techniques to leverage Tensor Cores in their scientific applications. Let’s look at a few examples discussed at SC18 on how researchers used Tensor Cores and mixed-precision for scientific computing.
Using Mixed-Precision for Earthquake Simulation
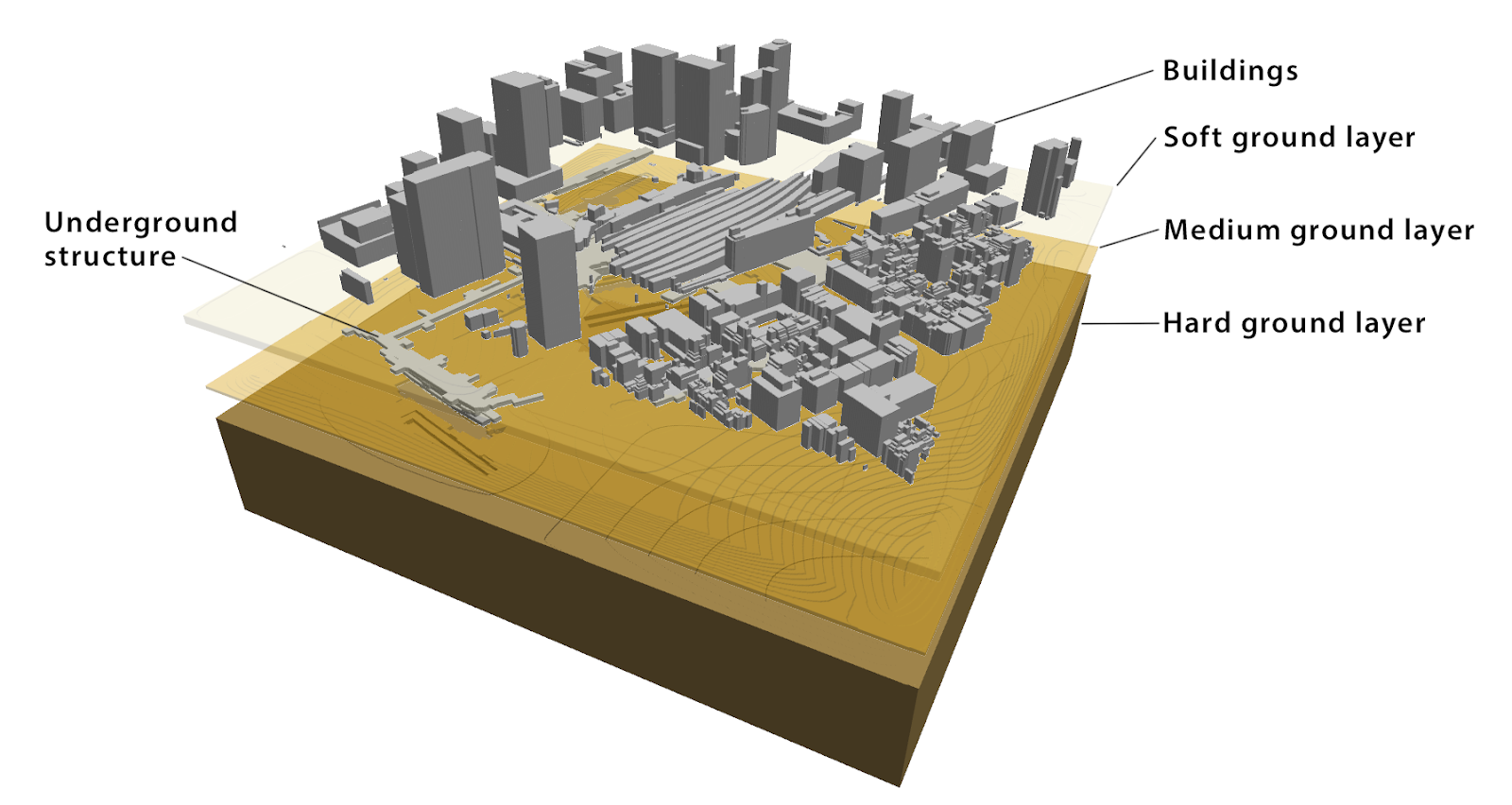
One of the Gordon Bell finalists simulates an earthquake using AI and transprecision computing (transprecision is synonymous with mixed-precision). Current seismic simulations can compute the properties of hard soil shaking deep underground. Scientists also want to include the shaking of soft soil near the surface as well as the building structures below and above the ground level, shown in figure 3. researchers from the University of Tokyo, Oak Ridge National Laboratory (ORNL), and the Swiss National Supercomputing Centre collaborated on this new solver, called MOTHRA (iMplicit sOlver wiTH artificial intelligence and tRAnsprecision computing). Running MOTHRA on the Summit supercomputer using a combination of AI and mixed-precision, MOTHRA achieved a 25x speed-up compared to the standard solver.
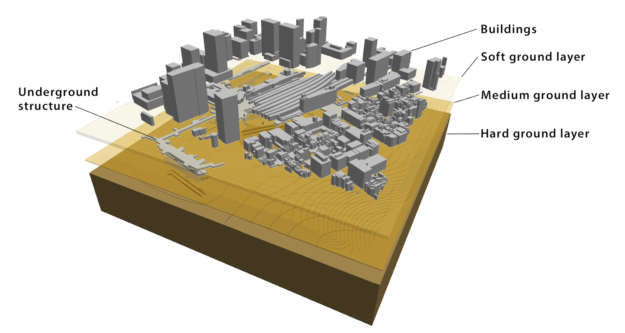
The simulation starts with 3D data of the various buildings in the city of Tokyo. The scientists simulate a seismic wave spreading through the city. The simulation includes hard soil, soft soil, underground malls, and subway systems in addition to the complicated buildings above ground. Nonlinear dynamic equations simulate the movement or displacement of the various buildings as a result of the seismic wave.
The size of the domain and the physics involved requires a system of equations with 302 billion unknowns that need to be solved iteratively until the solution converges. Fast solution of such a large system of equations requires a good preconditioner to reduce the computational cost. Researchers have been cautious about using lower precision in the past because the solutions take longer to converge. The researchers turned to AI to determine how to improve the effectiveness of their preconditioner by training a neural network on smaller models to help identify regions of slow convergence in their solver. This efficiently identified where to apply lower or higher precision to reduce the overall time to solution, a unique use of AI.
The researchers then use a combination FP64, FP32, FP21 and FP16 to further reduce the computational and communication costs. Using FP21 and FP16 when communicating across kernels and nodes reduces the amount of data that needs to be communicated between compute nodes and hence shortens the time it takes to obtain the solution.
Eventually, results from all lower precision calculations accelerated the FP64 calculations, still yielding the desired high precision and level of accuracy while taking less time. Using these techniques enabled MOTHRA to run 25x faster than a standard solver and 4x faster than GAMERA, the state-of-the-art SC14 Gordon Bell Finalist solver. This example demonstrates that using mixed-precision all the way down to FP16 may be a viable option and can be applied to other types of scientific simulations.
Using Tensor Core FP16 in Linear Algebra
While the use of lower precision is very common in AI models, some of the researchers from ICL/UTK explored the possibility of using tensor cores to accelerate one of the most common dense linear algebra routines without loss of precision. They achieved a 4x performance increase and 5x better energy efficiency versus the standard full FP64 implementation.
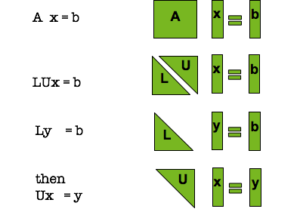
The following block diagram in figure 4 shows a simple flow for solving linear systems via LU factorization.
LU factorization steps for solving a linear system
The approach is very simple: use lower precision to compute the expensive flops and then iteratively refine the solution in order to achieve the FP64 solution.
Iterative refinement for dense systems, Ax = b, can work in a manner simlar to the pseudocode snippet below.
LU = lu(A) lower precision O(n3)
X - U\(L\b) lower precision O(n2)
r = b - Ax FP64 precision O(n2)
WHILE || r || not small enough
//Find a correction “z” to adjust x that satisfies Az=r
//Solving Az=r could be done by either
Z = U|(L\r) //Classical Iterative Refinement lower precision (On2)
GMRes preconditioned by the LU to solve Az=r //Iterative Refinement using GMRes lower precision (On2)
x = x + z //FP64 precision (On1)
r = b - Ax //FP64 precision (On2)
END
ICL/UTK announced the support of FP16 into the MAGMA (Matrix Algebra on GPU and Multicore Architectures) library at SC18. Since the performance of Tensor cores is so much faster then FP64, mixing FP64 plus FP16/FP32 enables the solver library to achieve up to 4x better performance.
A group of researchers from the University of Tennessee Innovative Computing Laboratory, ORNL, the University of Manchester School of Mathematics, and CUDA library engineers from NVIDIA presented their results at SC18, shown in figure 5. They demonstrated a 4x performance improvement in the paper “Harnessing GPU Tensor Cores for Fast FP16 Arithmetic to Speed up Mixed-Precision Iterative Refinement Solvers”. An updated version of the MAGMA library with support for Tensor Cores is available from the ICL at UTK., allowing the broader scientific community to experiment and incorporate them into their applications.
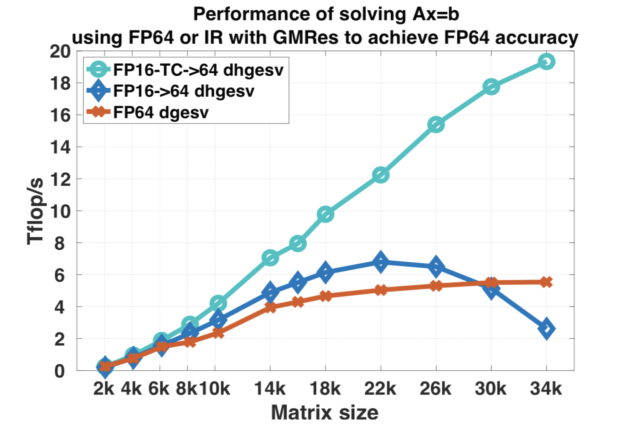
David Green, a computational physicist in the Theory and Modeling group of the Fusion and Materials for Nuclear Systems Division at ORNL, used the MAGMA library solver with Tensor Core support to accelerate his application by 3.5x. The plasma fusion application simulates the instabilities that occur inside a plasma inside the International Thermonuclear Experimental Reactor (ITER).
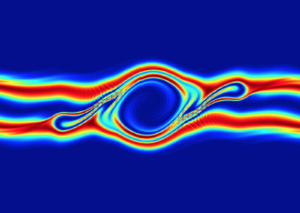
Orienting the application in a way that makes use of the FP16/Tensor cores made it possible to simulate the instability between plasma beams 3.5x times faster than previous results. David Greene presented his work at the American Physical Society – Division of Plasma Physics meeting in Portland recently. Figure 6 shows output from the simulation.
Conclusion
Mixed-precision computing modes allows us to reduce the resources required by using lower precision arithmetic in portions of the applications where FP64 is not required. However, mixed-precision computing with Tensor Cores GPUs is more than just replacing an FP64 calculation with an FP16 calculation. We are providing an FP64 solution accelerated with tensor cores that happen to use FP16 and FP32. This allows researchers to achieve comparable levels of accuracy to double-precision, while dramatically decreasing the required memory, application runtime, and system power consumption. There’s a growing number of examples where researchers are leveraging GPU Tensor Cores and mixed-precision computing to accelerate traditional FP64-based scientific computing applications by up to 25 times.
The latest NVIDIA Volta and Turing GPUs come with Tensor Cores that simplify and accelerate mixed precision AI even faster with support for automatic mixed precision in TensorFlow, PyTorch and MXNet. Interested in learning more or trying it out for yourself? Get Tensor Core optimized model scripts for popular AI frameworks from NGC. NGC also offers pre-trained modelsfor popular use cases and containers for DL frameworks, ML algorithms, and HPC and Visualization applications.
You may also find the SC18 presentation Harnessing Tensor Cores FP16 Arithmetic to Accelerate Linear Solvers and HPC Scientific Applications useful and interesting. Learn more by reading the Programming Tensor Cores using NVIDIA’s CUDA accelerated-computing API NVIDIA developer blog post. You can also read about the implementation of Tensor Cores in the Volta architecture if you want do dive a little deeper.